
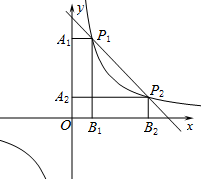
 如图,已知点P1(2,8)在反比例函数y1=$\frac{m}{x}$的图象上,一次函数y2=kx+t的图象经过点P1,并与反比例函数y1=$\frac{m}{x}$的图象交于第一象限的点P2(a,b).
如图,已知点P1(2,8)在反比例函数y1=$\frac{m}{x}$的图象上,一次函数y2=kx+t的图象经过点P1,并与反比例函数y1=$\frac{m}{x}$的图象交于第一象限的点P2(a,b).分析 (1)①将点P1代入反比例函数求得其解析式,由b=2得出点P2的坐标,根据P1、P2的坐标可得直线解析式;
②根据函数图象中反比例函数图象位于一次函数图象下方对应的x的范围可得;
(2)根据点P1、P2的坐标列出C1-C2关于a的解析式,再结合a的范围分类讨论可得.
解答 解:(1)①将点P1的坐标(2,8)代入y1=$\frac{m}{x}$,
得8=$\frac{m}{2}$,解得:m=16,
∴反比例函数的表达式为:y1=$\frac{16}{x}$.
∵b=2,P2(a,b)在反比例函数图象上,
∴$\frac{16}{a}$=2,解得:a=8.
将P1(2,8)、P2(8,2)代入y2=kx+t,
得$\left\{\begin{array}{l}2k+t=8\\ 8k+t=2\end{array}\right.$.
解得:$\left\{\begin{array}{l}{k=-1}\\{t=10}\end{array}\right.$,
∴y2=-x+10.
②不等式$\frac{m}{x}$<kx+t的解集为x<0或2<x<8.
(2)C1=2(2+8)=20,C2=2(a+$\frac{16}{a}$),
所以C2-C1=2(a+$\frac{16}{a}$)-20
=2•$\frac{{{a^2}-10a+16}}{a}$
=2•$\frac{{{{(a-5)}^2}-9}}{a}$
=2•$\frac{(a-2)(a-8)}{a}$.
∵a>2,
∴当2<a<8时,C2<C1;
当a=8时,C2=C1;
当a>8时,C2>C1.
点评 本题主要考查反比例函数与一次函数交点问题,熟练掌握待定系数法求函数解析式及分类讨论的思想是解题的关键.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:选择题
| A. | a<2 | B. | a>2 | C. | a<2,且a≠-4 | D. | a>2,且a≠4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 课题:测量古塔的高度 | ||
| 小明的研究报告 | 小红的研究报告 | |
| 图示 | 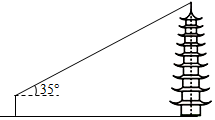 | 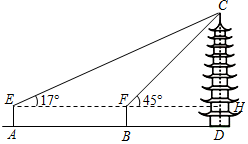 |
| 测量方案与测量数据 | 用距离地面高度为1.6m的测角器测出古塔顶端的仰角为35°,再用皮尺测得测角器所在位置与古塔底部边缘的最短距离为30m. | 在点A用距离地面高度为1.6m的测角器测出古塔顶端的仰角为17°,然后沿AD方向走58.8m到达点B,测出古塔顶端的仰角为45°. |
| 参考数据 | sin35°≈0.57,cos35°≈0.82,tan35°≈0.70 | sin17°≈0.29,cos17°≈0.96,tan17°≈0.30,$\sqrt{2}$≈1.41 |
| 计算古塔高度 (结果精确到0.1m) | 30×tan35°+1.6≈22.6(m) | |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 年份 | 2012 | 2013 | 2014 | 2015 | 2016 |
| 客流量(万人次) | 8192 | 8371 | 8613 | 8994 | 9400 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
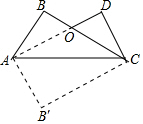 把长方形AB′CD沿对角线AC折叠,得到如图所示的图形,已知∠BAO=30°,
把长方形AB′CD沿对角线AC折叠,得到如图所示的图形,已知∠BAO=30°,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com