
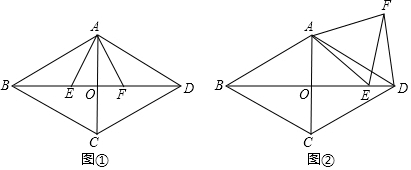
 如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD,BE.
如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD,BE.分析 (1)先求出四边形ADEC是平行四边形,根据平行四边形的性质推出即可;
(2)求出四边形BECD是平行四边形,求出CD=BD,根据菱形的判定推出即可;
(3)当∠A=45°,四边形BECD是正方形.
解答 (1)证明:∵DE⊥BC,
∴∠DFB=90°,
∵∠ACB=90°,
∴∠ACB=∠DFB,
∴AC∥DE,
∵MN∥AB,即CE∥AD,
∴四边形ADEC是平行四边形,
∴CE=AD;
(2)解:四边形BECD是菱形,
理由是:∵D为AB中点,
∴AD=BD,
∵CE=AD,
∴BD=CE,
∵BD∥CE,
∴四边形BECD是平行四边形,
∵∠ACB=90°,D为AB中点,
∴CD=BD,
∴四边形BECD是菱形;
(3)当∠A=45°时,∵∠ACB=90°,
∴∠ABC=45°,
由(2)可知,四边形BECD是菱形,
∴∠ABC=∠CBE=45°,
∴∠DBE=90°,
∴四边形BECD是正方形.
点评 本题考查了平行四边形的性质和判定,菱形的判定,正方形的判定、直角三角形的性质的应用,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
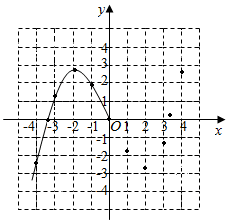 某学习小组在研究函数y=$\frac{1}{6}$x3-2x的图象与性质时,已列表、描点并画出了图象的一部分.
某学习小组在研究函数y=$\frac{1}{6}$x3-2x的图象与性质时,已列表、描点并画出了图象的一部分.| x | … | -4 | -3.5 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 3.5 | 4 | … |
| y | … | -$\frac{8}{3}$ | -$\frac{7}{48}$ | $\frac{3}{2}$ | $\frac{8}{3}$ | $\frac{11}{6}$ | 0 | -$\frac{11}{6}$ | -$\frac{8}{3}$ | -$\frac{3}{2}$ | $\frac{7}{48}$ | $\frac{8}{3}$ | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
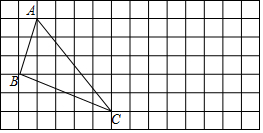 如图,网格中的小正方形都是边长为1个单位长度的小正方形.
如图,网格中的小正方形都是边长为1个单位长度的小正方形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
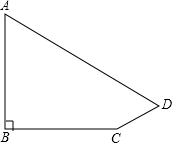 如图,学校旗杆附近有一斜坡,小明准备测量学校旗杆AB的高度,他发现当斜坡正对着太阳时,旗杆AB的影子恰好落在水平地面和斜坡的坡面上,此时小明测得水平地面上的影长BC=16米,斜坡坡面上的影长CD=4米,太阳光线AD与水平地面成30°角,斜坡CD与水平地面BC成30°的角.求旗杆AB的高度.($\sqrt{3}$=1.732,精确到1米)
如图,学校旗杆附近有一斜坡,小明准备测量学校旗杆AB的高度,他发现当斜坡正对着太阳时,旗杆AB的影子恰好落在水平地面和斜坡的坡面上,此时小明测得水平地面上的影长BC=16米,斜坡坡面上的影长CD=4米,太阳光线AD与水平地面成30°角,斜坡CD与水平地面BC成30°的角.求旗杆AB的高度.($\sqrt{3}$=1.732,精确到1米)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com