
����Ŀ����һ����ѧ����У�ij��ѧС��̽�����λ�̳����ͼ��ʾ������ķ������������¹��ߣ��پ��ߣ���ֱ��EF����T�ͳߣ�CD���ڵ�ֱ�ߴ�ֱƽ���߶�AB����
��1����ͼ1�У����㻭����T�γ��Ҵ�ԲԲ�ĵ�ʾ��ͼ��������ͼ�ۼ�����д��������
��2����ͼ2��С��˵������ֻ��һ��ֱ����һ�����߾Ϳ���������λ�̳������������������£�
��ֱ�����õ���СԲ���У��þ���������ʱֱ�����Բ������M��N֮��ľ��룬�Ϳ�������λ�̳�������������MN=10m���������������λ�̳�������

 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����E��F��G�ֱ��ǵȱ�������ABC����AB��BC��CA�ϵĶ��㣬��ʼ�ձ���AE=BF=CG������EFG�����Ϊy��AE�ij�Ϊx��y����x�ĺ���ͼ�����Ϊͼ2��ʾ����ȱ�������ABC�ı߳�Ϊ___��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪:��ͼ����1+ ��2=180�� �ԡ�A= ��D.��֤:AB//CD.(��ÿ��֤�����̺���ע������)

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧΪ�˽�ѧ����У��ͨ��ʽ����������ȡ���꼶����ѧ���͡�����ѧ��ͨ��ʽ�������ʾ����飬�����Ϊ��A�������г���B�����У�C������������D����������������������ݵ��������Ƴ���������ͳ��ͼ����ͼ�٣��Ͳ�������ͳ��ͼ����ͼ�ڣ��������ͼ�е���Ϣ�������������.
��1�����ε��鹲��ȡ ��ѧ����
��2���������ͳ��ͼ�С�C���������ε�Բ�ĽǵĶ�������������ͳ��ͼ����������
��3��������ѧ����ѧ��3000�ˣ������ж���ѧ��������ѧ��ͨ��ʽ��ѡ������������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
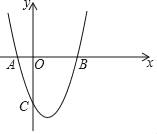
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�������y=ax2+bx+c��a��0����x���ཻ�ڵ�A����1��0���͵�B����y�ύ�ڵ�C���Գ���Ϊֱ��x=1��
��1�����C�����꣨�ú�a�Ĵ���ʽ��ʾ����
��2������AC��BC������ABC�����Ϊ6����������ߵı���ʽ��
��3���ڵڣ�2��С��������£���QΪx����������һ�㣬��G���C����F���A���ڵ�Q�����ĶԳƣ�����CGFΪֱ��������ʱ�����Q�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AD�Ǹߣ�CE�����ߣ�DG��ֱƽ��CE������DE��
��1����֤��DC��BE��
��2������AEC��72�������BCE�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ɸ���״����С��ȫ��ͬ�ľ���ֽƬΧ�������Σ�4������ֽƬΧ����ͼ����ʾ�������Σ�����Ӱ���ֵ����Ϊ12��8������ֽƬΧ����ͼ����ʾ�������Σ�����Ӱ���ֵ����Ϊ8��12������ֽƬΧ����ͼ����ʾ�������Σ�����Ӱ���ֵ����Ϊ__��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
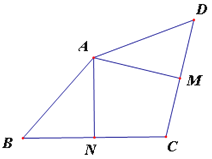
����Ŀ����ͼ�����ı���ABCD�У�M��N�ֱ���CD��BC���е㣬��AM��CD��AN��BC��
��1����֤����BAD=2��MAN��
��2������BD������MAN=70�㣬��DBC=40�������ADC��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,������y=-![]() x2+
x2+![]() x+
x+![]() ��x�ύ�ڵ�A,B(��A�ڵ�B�����),��y�ύ�ڵ�C.
��x�ύ�ڵ�A,B(��A�ڵ�B�����),��y�ύ�ڵ�C.
(1)���A,B,C������;
(2)���������ߵĶ����ǵ�D,���ı���OCDB�����;
(3)��֪��P�Ǹ������߶Գ����һ��,���Ե�P,O,DΪ������������ǵ���������,��ֱ��д����P������.(����˵��)

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com