
【题目】如图是数值转换机的示意图,小明按照其对应关系画出了y与x的函数图象(如图):
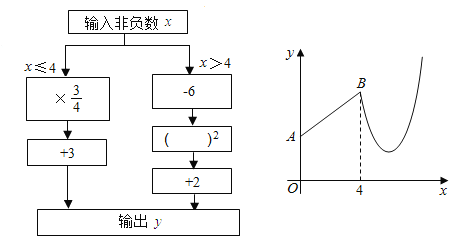
(1)分别写出当0≤x≤4与x>4时,y与x的函数关系式:
(2)求出所输出的y的值中最小一个数值;
(3)写出当x满足什么范围时,输出的y的值满足3≤y≤6.
【答案】(1)当![]() 时,y=
时,y=![]() x+3; 当
x+3; 当![]() 时 y=(x-6)2+2
时 y=(x-6)2+2
(2)最小值2 (3) 0≤x≤5或7≤x≤8
【解析】
(1)当0≤x≤4时,函数关系式为y=![]() x+3;当x>4时,函数关系式为y=(x﹣6)2+2;
x+3;当x>4时,函数关系式为y=(x﹣6)2+2;
(2)根据一次函数与二次函数的性质,分别求出自变量在其取值范围内的最小值,然后比较即可;
(3)由题意,可得不等式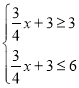 和
和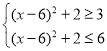 ,解答出x的值即可.
,解答出x的值即可.
解:(1)由图可知,
当0≤x≤4时,y=![]() x+3;
x+3;
当x>4时,y=(x﹣6)2+2;
(2)当0≤x≤4时,y=![]() x+3,此时y随x的增大而增大,
x+3,此时y随x的增大而增大,
∴当x=0时,y=![]() x+3有最小值,为y=3;
x+3有最小值,为y=3;
当x>4时,y=(x﹣6)2+2,y在顶点处取最小值,
即当x=6时,y=(x﹣6)2+2的最小值为y=2;
∴所输出的y的值中最小一个数值为2;
(3)由题意得,当0≤x≤4时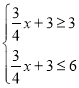 ,
,
解得,0≤x≤4;
当x>4时,
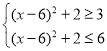 ,
,
解得,4≤x≤5或7≤x≤8;
综上,x的取值范围是:0≤x≤5或7≤x≤8.


 每课必练系列答案
每课必练系列答案科目:初中数学 来源: 题型:
【题目】根据规定,我市将垃圾分为了四类:可回收物、易腐垃圾、有害垃圾和其他垃圾四大类. 现有投放这四类垃圾的垃圾桶各1个,若将用不透明垃圾袋分类打包好的两袋不同垃圾随机投进两个不同的垃圾桶,投放正确的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】通达桥即小店汾河桥,是太原新建成的一座跨汾大桥,也是太原首座悬索桥.桥的主塔由曲线形拱门组成,取意“时代之门”.无人机社团的同学计划利用无人机设备测量通达桥拱门的高度.如图,他们先将无人机升至距离桥面50米高的点C处,测得桥的拱门最高点A的仰角∠ACF为30°,再将无人机从C处竖直向上升高200米到点D处,测得点A的俯角∠ADG为45°.已知点A,B,C,D,E在同一平面内,求通达桥拱门最高点A距离桥面BE的高度AB.(结果保留整数,参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
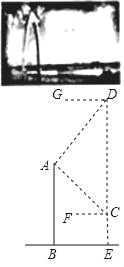
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+3经过点A(﹣1,0),B(3,0),与y轴交于点C.点D(xD,yD)为抛物线上一个动点,其中1<xD<3.连接AC,BC,DB,DC.
(1)求该抛物线的解析式;
(2)当△BCD的面积等于△AOC的面积的2倍时,求点D的坐标;
(3)在(2)的条件下,若点M是x轴上一动点,点N是抛物线上一动点,试判断是否存在这样的点M,使得以点B,D,M,N为顶点的四边形是平行四边形.若存在,求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某数学活动小组选定测量小河对岸大树BC的高度,他们在斜坡上D处测得大树顶端B的仰角是30°,朝大树方向下坡走6米到达坡底A处,在A处测得大树顶端B的仰角是45°,若坡角∠FAE=30°,求大树的高度(结果保留根号).
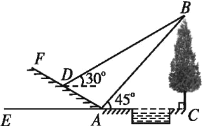
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C在圆O上,BE⊥CD垂足为E,CB平分∠ABE,连接BC
(1)求证:CD为⊙O的切线;
(2)若cos∠CAB=![]() ,CE=
,CE=![]() ,求AD的长.
,求AD的长.
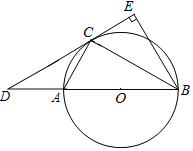
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BC是路边坡角为30°,长为10米的一道斜坡,在坡顶灯杆CD的顶端D处有一探射灯,射出的边缘光线DA和DB与水平路面AB所成的夹角∠DAN和∠DBN分别是37°和60°(图中的点A、B、C、D、M、N均在同一平面内,CM∥AN).
(1)求灯杆CD的高度;
(2)求AB的长度(结果精确到0.1米).(参考数据:![]() =1.73.sin37°≈060,cos37°≈0.80,tan37°≈0.75)
=1.73.sin37°≈060,cos37°≈0.80,tan37°≈0.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装店老板到厂家选购![]() 、
、![]() 两种品牌的羽绒服,
两种品牌的羽绒服,![]() 品牌羽绒服每件进价比
品牌羽绒服每件进价比![]() 品牌羽绒服每件进价多
品牌羽绒服每件进价多![]() 元,若用
元,若用![]() 元购进
元购进![]() 种羽绒服的数量是用
种羽绒服的数量是用![]() 元购进
元购进![]() 种羽绒服数量的
种羽绒服数量的![]() 倍.
倍.
(1)求![]() 、
、![]() 两种品牌羽绒服每件进价分别为多少元?
两种品牌羽绒服每件进价分别为多少元?
(2)若![]() 品牌羽绒服每件售价为
品牌羽绒服每件售价为![]() 元,
元,![]() 品牌羽绒服每件售价为
品牌羽绒服每件售价为![]() 元,服装店老板决定一次性购进
元,服装店老板决定一次性购进![]() 、
、![]() 两种品牌羽绒服共
两种品牌羽绒服共![]() 件,在这批羽绒服全部出售后所获利润不低于
件,在这批羽绒服全部出售后所获利润不低于![]() 元,则最少购进
元,则最少购进![]() 品牌羽绒服多少件?
品牌羽绒服多少件?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com