15.阅读材料:
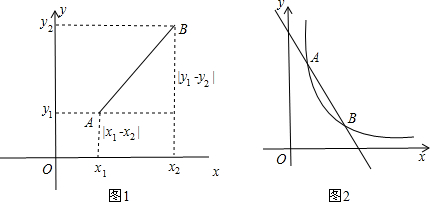
如图1,在平面直角坐标系中,O为坐标原点,对于任意两点A (x
1,y
1),B(x
2,y
2),由勾股定理可得:AB
2=(x
1-x
2)
2+(y
1-y
2)
2,我们把$\sqrt{({x}_{1}-{x}_{2})^{2}+({y}_{1}-{y}_{2})^{2}}$叫做A、B两点之间的距离,记作AB=$\sqrt{({x}_{1}-{x}_{2})^{2}+({y}_{1}-{y}_{2})^{2}}$
例题:在平面直角坐标系中,O为坐标原点,设点P(x,0).
①A(0,2),B (3,-2),则AB=5.;PA=$\sqrt{{x}^{2}+4}$.;
解:由定义有AB=$\sqrt{(0-3)^{2}+[2-(-2)]^{2}}=5$;PA=$\sqrt{(x-3)^{2}+(0-2)^{2}}=\sqrt{{x}^{2}+4}$.
②$\sqrt{(x-1)^{2}+4}$表示的几何意义是点P(x,0)到点(1,2)的距
离;$\sqrt{{x}^{2}+1}+\sqrt{(x-2)^{2}+9}$表示的几何意义是点P(x,0)分别到点(0,1)和点(2,3)的距离和.
解:因为$\sqrt{(x-1)^{2}+4}=\sqrt{(x-1)^{2}+(0-2)^{2}}$,所以$\sqrt{(x-1)^{2}+4}$表示的几何意义是点P(x,0)到点(1,2)的距
离;同理可得,$\sqrt{{x}^{2}+1}+\sqrt{(x-2)^{2}+9}$表示的几何意义是点P(x,0)分别到点(0,1)和点(2,3)的距离和.
根据以上阅读材料,解决下列问题:
(1)如图2,已知直线y=-2x+8与反比例函数y=$\frac{6}{x}$(x>0)的图象交于A(x
1,y
1)、B(x
2,y
2)两点,
则点A、B的坐标分别为A(1,6),B(3,2),AB=2$\sqrt{5}$.
(2)在(1)的条件下,设点P(x,0),则$\sqrt{(x-{x}_{1})^{2}+{y}_{1}^{2}}+\sqrt{(x-{x}_{2})^{2}+{y}_{2}^{2}}$表示的几何意义是点P(x,0)分别到点(1,6)和点(3,2)的距离和;试求$\sqrt{(x-{x}_{1})^{2}+{y}_{1}^{2}}+\sqrt{(x-{x}_{2})^{2+{y}_{2}^{2}}}$的最小值,以及取得最小值时点P的坐标.