

 或40
或40 或100
或100
 ①,
①, ②,
②,
 ①,
①, ②,
②,

 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:初中数学 来源:不详 题型:解答题
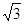 cm ,BC=6cm,经过A,B的直线l以1cm/秒的速度向下作匀速平移运动,交BC于点B′,交CD于点 D′,与此同时,点P从点B′ 出发,在直线l上以1cm/秒的速度沿直线l向右下方向作匀速运动.设它们运动的时间为t秒.
cm ,BC=6cm,经过A,B的直线l以1cm/秒的速度向下作匀速平移运动,交BC于点B′,交CD于点 D′,与此同时,点P从点B′ 出发,在直线l上以1cm/秒的速度沿直线l向右下方向作匀速运动.设它们运动的时间为t秒.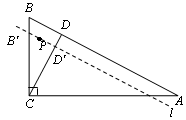
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
 ,把△ABC绕点A 按顺时针方向旋转n 度后恰好与△ADE重合,则n的值是 ,点C经过的路线的长是 ,线段BC在上述旋转过程中所扫过部分的面积是 .
,把△ABC绕点A 按顺时针方向旋转n 度后恰好与△ADE重合,则n的值是 ,点C经过的路线的长是 ,线段BC在上述旋转过程中所扫过部分的面积是 .
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
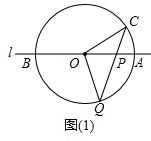
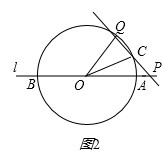
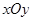 中,原点O是正三角形ABC外接圆的圆心,点A在
中,原点O是正三角形ABC外接圆的圆心,点A在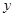 轴的正半轴上,△ABC的边长为6.以原点O为旋转中心将△ABC沿逆时针方向旋转角,得到△
轴的正半轴上,△ABC的边长为6.以原点O为旋转中心将△ABC沿逆时针方向旋转角,得到△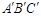 ,点
,点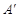 、
、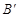 、
、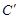 分别为点A、B、C的对应点.
分别为点A、B、C的对应点.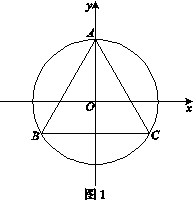
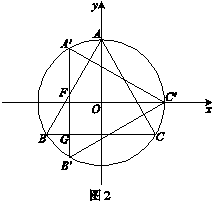
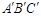 ;
;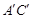 、
、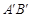 交于点D、E,则DE的长为_______;
交于点D、E,则DE的长为_______; 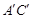 ⊥AB时,
⊥AB时,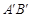 分别与AB、BC交于点F、G,则点
分别与AB、BC交于点F、G,则点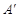 的坐标为 _____,△FBG的周长为_____,△ABC与△
的坐标为 _____,△FBG的周长为_____,△ABC与△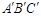 重叠部分的面积为_______.
重叠部分的面积为_______.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com