
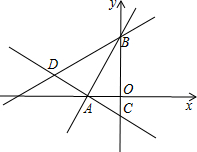
 如图所示,在平面直角坐标系中,过点A(-$\sqrt{3}$,0)的两条直线分别交y轴于B、C两点,且B、C两点的纵坐标分别是一元二次方程x2-2x-3=0的两个根
如图所示,在平面直角坐标系中,过点A(-$\sqrt{3}$,0)的两条直线分别交y轴于B、C两点,且B、C两点的纵坐标分别是一元二次方程x2-2x-3=0的两个根分析 (1)解出方程后,即可求出B、C两点的坐标,即可求出BC的长度;
(2)由A、B、C三点坐标可知OA2=OC•OB,所以可证明△AOC∽△BOA,利用对应角相等即可求出∠CAB=90°;
(3)容易求得直线AC的解析式,由DB=DC可知,点D在BC的垂直平分线上,所以D的纵坐标为1,将其代入直线AC的解析式即可求出D的坐标;
(4)A、B、P三点为顶点的三角形是等腰三角形,可分为以下三种情况:①AB=AP;②AB=BP;③AP=BP;然后分别求出P的坐标即可.
解答 (1)∵x2-2x-3=0,
∴x=3或x=-1,
∴B(0,3),C(0,-1),
∴BC=4,
(2)∵A(-$\sqrt{3}$,0),B(0,3),C(0,-1),
∴OA=$\sqrt{3}$,OB=3,OC=1,
∴OA2=OB•OC,
∵∠AOC=∠BOA=90°,
∴△AOC∽△BOA,
∴∠CAO=∠ABO,
∴∠CAO+∠BAO=∠ABO+∠BAO=90°,
∴∠BAC=90°,
∴AC⊥AB;
(3)设直线AC的解析式为y=kx+b,
把A(-$\sqrt{3}$,0)和C(0,-1)代入y=kx+b,
∴$\left\{\begin{array}{l}{-1=b}\\{0=-\sqrt{3}k+b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-\frac{\sqrt{3}}{3}}\\{b=-1}\end{array}\right.$,
∴直线AC的解析式为:y=-$\frac{\sqrt{3}}{3}$x-1,
∵DB=DC,
∴点D在线段BC的垂直平分线上,
∴D的纵坐标为1,
∴把y=1代入y=-$\frac{\sqrt{3}}{3}$x-1,
∴x=-2$\sqrt{3}$,
∴D的坐标为(-2$\sqrt{3}$,1),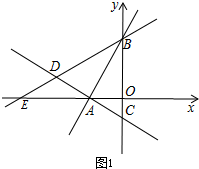
(4)设直线BD的解析式为:y=mx+n,直线BD与x轴交于点E,
把B(0,3)和D(-2$\sqrt{3}$,1)代入y=mx+n,
∴$\left\{\begin{array}{l}{n=3}\\{1=-2\sqrt{3}m+n}\end{array}\right.$,
解得$\left\{\begin{array}{l}{m=\frac{\sqrt{3}}{3}}\\{n=3}\end{array}\right.$,
∴直线BD的解析式为:y=$\frac{\sqrt{3}}{3}$x+3,
令y=0代入y=$\frac{\sqrt{3}}{3}$x+3,
∴x=-3$\sqrt{3}$,
∴E(-3$\sqrt{3}$,0),
∴OE=3$\sqrt{3}$,
∴tan∠BEC=$\frac{OB}{OE}$=$\frac{\sqrt{3}}{3}$,
∴∠BEO=30°,
同理可求得:∠ABO=30°,
∴∠ABE=30°,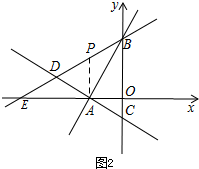
当PA=AB时,如图1,
此时,∠BEA=∠ABE=30°,
∴EA=AB,
∴P与E重合,
∴P的坐标为(-3$\sqrt{3}$,0),
当PA=PB时,如图2,
此时,∠PAB=∠PBA=30°,
∵∠ABE=∠ABO=30°,
∴∠PAB=∠ABO,
∴PA∥BC,
∴∠PAO=90°,
∴点P的横坐标为-$\sqrt{3}$,
令x=-$\sqrt{3}$代入y=$\frac{\sqrt{3}}{3}$x+3,
∴y=2,
∴P(-$\sqrt{3}$,2),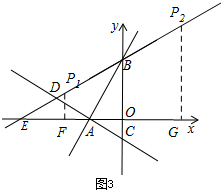
当PB=AB时,如图3,
∴由勾股定理可求得:AB=2$\sqrt{3}$,EB=6,
若点P在y轴左侧时,记此时点P为P1,
过点P1作P1F⊥x轴于点F,
∴P1B=AB=2$\sqrt{3}$,
∴EP1=6-2$\sqrt{3}$,
∴sin∠BEO=$\frac{F{P}_{1}}{E{P}_{1}}$,
∴FP1=3-$\sqrt{3}$,
令y=3-$\sqrt{3}$代入y=$\frac{\sqrt{3}}{3}$x+3,
∴x=-3,
∴P1(-3,3-$\sqrt{3}$),
若点P在y轴的右侧时,记此时点P为P2,
过点P2作P2G⊥x轴于点G,
∴P2B=AB=2$\sqrt{3}$,
∴EP2=6+2$\sqrt{3}$,
∴sin∠BEO=$\frac{G{P}_{2}}{E{P}_{2}}$,
∴GP2=3+$\sqrt{3}$,
令y=3+$\sqrt{3}$代入y=$\frac{\sqrt{3}}{3}$x+3,
∴x=3,
∴P2(3,3+$\sqrt{3}$),
综上所述,当A、B、P三点为顶点的三角形是等腰三角形时,点P的坐标为(-3$\sqrt{3}$,0),(-$\sqrt{3}$,2),(-3,3-$\sqrt{3}$),(3,3+$\sqrt{3}$).
点评 本题考查二次函数的综合问题,涉及一元二次方程的解法,相似三角形的判定,等腰三角形的性质,垂直平分线的判定等知识,内容较为综合,需要学生灵活运用所知识解决.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:选择题
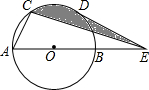 如图所示,在半径为2cm的⊙O中,点C、点D是$\widehat{AB}$的三等分点,点E是直径AB的延长线上一点,连结CE、DE,则图中阴影部分的面积是( )
如图所示,在半径为2cm的⊙O中,点C、点D是$\widehat{AB}$的三等分点,点E是直径AB的延长线上一点,连结CE、DE,则图中阴影部分的面积是( )| A. | $\sqrt{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{2π}{3}$-$\sqrt{3}$ | D. | $\frac{2π}{3}$+$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 乙 | B. | 甲 | C. | 甲、乙都行 | D. | 无法判断 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
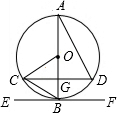 如图,AB为⊙O的直径,AB=6,AB⊥弦CD,垂足为G,EF切⊙O于点B,∠A=30°,连接AD、OC、BC,下列结论不正确的是( )
如图,AB为⊙O的直径,AB=6,AB⊥弦CD,垂足为G,EF切⊙O于点B,∠A=30°,连接AD、OC、BC,下列结论不正确的是( )| A. | EF∥CD | B. | △COB是等边三角形 | ||
| C. | CG=DG | D. | $\widehat{BC}$的长为$\frac{3}{2}$π |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com