
【题目】△ABC中,AB=AC,点D为BC上一点,且DA=DB,此时△ACD也恰好为等腰三角形,则∠BAC=_____.
【答案】90°或108°
【解析】
根据等腰三角形的性质得到∠B=∠C,∠BAD=∠B,由△ACD也恰好为等腰三角形,如图1,当AD=CD,于是得到∠CAD=∠C,求得∠BAC=![]() ×180°=90°,如图2,当AC=CD,根据等腰三角形的性质得到∠CAD=∠ADC,由三角形的外角的性质得到∠ADC=∠B+∠BAD=2∠B,根据三角形的内角和列方程得到∠C+2∠C+2∠C=180°,求得∠C=36°,即可得到结论.
×180°=90°,如图2,当AC=CD,根据等腰三角形的性质得到∠CAD=∠ADC,由三角形的外角的性质得到∠ADC=∠B+∠BAD=2∠B,根据三角形的内角和列方程得到∠C+2∠C+2∠C=180°,求得∠C=36°,即可得到结论.
解:∵AB=AC,
∴∠B=∠C,
∵AD=BD,
∴∠BAD=∠B,
∵△ACD也恰好为等腰三角形,
①如图1,当AD=CD,
∴∠CAD=∠C,
∴∠BAC=![]() ×180°=90°,
×180°=90°,
②如图2,当AC=CD,
∴∠CAD=∠ADC,
∵∠ADC=∠B+∠BAD=2∠B,
∵∠C+∠BAD+∠ADC=180°,
∴∠C+2∠C+2∠C=180°,
∴∠C=36°,
∴∠BAD=36°,∠CAD=72°,
∴∠BAC=108°.
故答案为:90°或108°.




科目:初中数学 来源: 题型:
【题目】已知:如图,ABCD是一块边长为2米的正方形铁板,在边AB上选取一点M,分别以AM和MB为边截取两块相邻的正方形板料. 当AM的长为何值时,截取两块相邻的正方形板料的总面积最小?

查看答案和解析>>
科目:初中数学 来源: 题型:
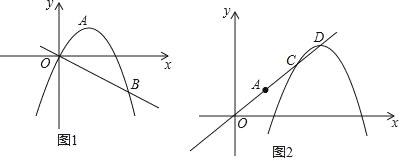
【题目】如图1,已知抛物线y=﹣x2+mx+m﹣2的顶点为A,且经过点B(3,﹣3).
(1)求顶点A的坐标
(2)若P是抛物线上且位于直线OB上方的一个动点,求△OPB的面积的最大值及比时点P的坐标;
(3)如图2,将原抛物线沿射线OA方向进行平移得到新的抛物线,新抛物线与射线OA交于C,D两点,请问:在抛物线平移的过程中,线段CD的长度是否为定值?若是,请求出这个定值;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们已经学习过多项式除以单项式,多项式除以多项式一般可用竖式计算,步骤如下:
①把被除式、除式按某个字母作降幂排列,并把所缺的项用零补齐;
②用被除式的第一项除以除式第一项,得到商式的第一项;
③用商式的第一项去乘除式,把积写在被除式下面(同类项对齐),消去相等项;
④把减得的差当作新的被除式,再按照上面的方法继续演算,直到余式为零或余式的次数低于除式的次数时为止,被除式=除式×商式+余式.若余式为零,说明这个多项式能被另一个多项式整除.
例如:计算(6x4﹣7x3﹣x2﹣1)÷(2x+1),可用竖式除法如图:
所以6x4﹣7x3﹣x2﹣1除以2x+1,商式为3x3﹣5x2+2x﹣1,余式为0.
根据阅读材料,请回答下列问题(直接填空):

(1)(2x3+x﹣3)÷(x﹣1)= ;
(2)(4x2﹣4xy+y2+6x﹣3y﹣10)÷(2x﹣y+5)= ;
(3)[(x﹣2)(x﹣3)+1]÷(x﹣1)的余式为 ;
(4)x3+ax2+bx﹣15能被x2﹣2x+3整除,则a= ,b= .
查看答案和解析>>
科目:初中数学 来源: 题型:
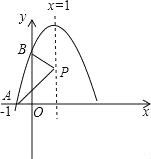
【题目】已知抛物线y=ax2+bx+3在坐标系中的位置如图所示,它与x,y轴的交点分别为A,B,P是其对称轴x=1上的动点,根据图中提供的信息,给出以下结论:①2a+b=0,②x=3是ax2+bx+3=0的一个根,③△PAB周长的最小值是![]() +3
+3![]() .其中正确的是( )
.其中正确的是( )
A. ①②③ B. 仅有①② C. 仅有①③ D. 仅有②③
查看答案和解析>>
科目:初中数学 来源: 题型:
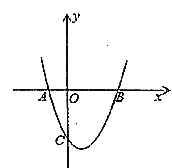
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点.
两点.
(1)求该抛物线的解析式;
(2)抛物线的对称轴上是否存在一点![]() ,使
,使![]() 的周长最小?若存在,请求出点
的周长最小?若存在,请求出点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
(3)设抛物线上有一个动点![]() ,当点
,当点![]() 在该抛物线上滑动到什么位置时,满足
在该抛物线上滑动到什么位置时,满足![]() ,并求出此时点
,并求出此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
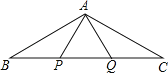
【题目】已知:如图,△ABC中,P、Q两点分别是边AB和AC的垂直平分线与BC的交点,连结AP和AQ,且BP=PQ=QC.求∠C的度数.
证明:∵P、Q两点分别是边AB和AC的垂直平分线与BC的交点,
∴PA= ,QC=QA.
∵BP=PQ=QC,
∴在△APQ中,PQ= (等量代换)
∴△APQ是 三角形.
∴∠AQP=60°,
∵在△AQC中,QC=QA,
∴∠C=∠ .
又∵∠AQP是△AQC的外角,
∴∠AQP=∠ +∠ =60°.(三角形的一个外角等于与它不相邻的两个内角的和)
∴∠C= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,△ABC中,AB=AC,∠B、∠C的平分线交于O点,过O点作EF∥BC交AB、AC于E、F.
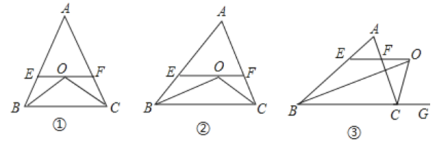
(1)图①中有几个等腰三角形?猜想:EF与BE、CF之间有怎样的关系.
(2)如图②,若AB≠AC,其他条件不变,图中还有等腰三角形吗?如果有,分别指出它们.在第(1)问中EF与BE、CF间的关系还存在吗?
(3)如图③,若△ABC中∠B的平分线BO与三角形外角平分线CO交于O,过O点作OE∥BC交AB于E,交AC于F.这时图中还有等腰三角形吗?EF与BE、CF关系又如何?说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知点![]() ,试分别根据下列条件,求出点
,试分别根据下列条件,求出点![]() 的坐标。
的坐标。
(1)点![]() 在
在![]() 轴上;
轴上;
(2)点![]() 横坐标比纵坐标大3;
横坐标比纵坐标大3;
(3)点![]() 在过
在过![]() 点,且与
点,且与![]() 轴平行的直线上。
轴平行的直线上。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com