
在等腰梯形ABCD中,AB∥DC,∠A=45°,AB=10 cm,CD=4 cm.等腰直角三角形PMN的斜边MN=10 cm,A点与N点重合,MN和AB在一条直线上,设等腰梯形ABCD不动,等腰直角三角形PMN沿AB所在直线以1 cm/s的速度向右移动,直到点N与点B重合为止.
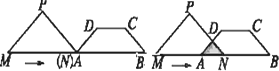
(1)等腰直角三角形PMN在整个移动过程中与等腰梯形ABCD重叠部分的形状由________变化为________;
(2)设当等腰直角三角形PMN移动x(s)时,等腰直角三角形PMN与等腰梯形ABCD重叠部分的面积为y(cm2):
①当x=6 s时,则y的值是________cm2;(直接写出答案,不必写出过程)
②求x为何值时,y=4 cm2;(要求写出过程)
③当x=_______s时,y=15 cm2.(直接写出答案,不必写出过程)
|
解:(1)等腰直角三角形 等腰梯形 (2)等腰直角三角形PMN在整个移动过程中与等腰梯形ABCD重叠部分图形的形状可分为以下两种情况: 0<x≤6 6<x≤10 ①9 ②当0<x≤6时,重叠部分的形状为等腰直角三角形EAN(如图①).
此时AN=x(cm),过点E作EH⊥AB于点H,则EH平分AN, ∴EH= 则y=S△ANE= ∴ 解得x1=4 x2=-4(不合题意,舍去) ∴x=4 ∴当x=4(s)时,等腰直角三角形PMN与等腰梯形ABCD重叠部分的面积是4 cm2. ③8 解答提示:当6<x≤10时,重叠部分的形状是等腰梯形ANED(如图②). 此时AN=x(cm),∵∠PNM=∠B=45°,∴EN∥BC. ∵CE∥BN,∴四边形ENBC是平行四边形,CE=BN=10-x,DE=4-(10-x)=x-6. 过点D作DF⊥AB于F,过点C作CG⊥AB于G,则AF=BG,DF=AF= ∴y=S梯形ANED= ∴3x-9=15.解得x=8. |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
 25、如图所示,在等腰梯形ABCD中,AD∥BC,AB=CD,点P为BC边上任意一点,且
25、如图所示,在等腰梯形ABCD中,AD∥BC,AB=CD,点P为BC边上任意一点,且查看答案和解析>>
科目:初中数学 来源: 题型:
 24、已知:如图,在等腰梯形ABCD中,AD∥BC,AB=DC,点E为边BC上一点,且AE=DC.
24、已知:如图,在等腰梯形ABCD中,AD∥BC,AB=DC,点E为边BC上一点,且AE=DC.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在等腰梯形ABCD中,AD∥BC,AB=CD,AC⊥BD,垂足为O,过D作DE∥AC交BC的延长线于E.
如图,在等腰梯形ABCD中,AD∥BC,AB=CD,AC⊥BD,垂足为O,过D作DE∥AC交BC的延长线于E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com