
分析 分两种情况进行讨论:线段AO的对称线段在第一象限,线段AO的对称线段在第三象限,分别根据轴对称的性质,运用待定系数法即可求得m的值,再根据线段O′A′与反比例函数y=$\frac{8}{x}$恰有一个公共点,即可得到m的取值范围.
解答 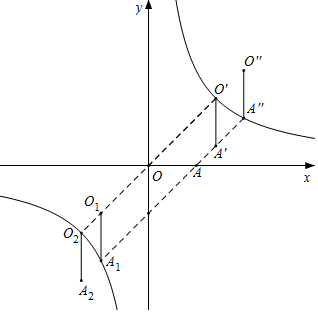 解:如图所示,当O的对称点O'落在反比例函数的图象上时,
解:如图所示,当O的对称点O'落在反比例函数的图象上时,
根据直线OO'与直线y=-x+m互相垂直,可得直线OO'为y=x,
解方程组$\left\{\begin{array}{l}{y=x}\\{y=\frac{8}{x}}\end{array}\right.$,可得$\left\{\begin{array}{l}{x=2\sqrt{2}}\\{y=2\sqrt{2}}\end{array}\right.$,或$\left\{\begin{array}{l}{x=-2\sqrt{2}}\\{y=-2\sqrt{2}}\end{array}\right.$,
∴O'(2$\sqrt{2}$,2$\sqrt{2}$),O2(-2$\sqrt{2}$,-2$\sqrt{2}$),
∴线段OO'的中点坐标为($\sqrt{2}$,$\sqrt{2}$),
把($\sqrt{2}$,$\sqrt{2}$)代入直线y=-x+m,可得m=2$\sqrt{2}$,
如图,当A的对称点A“落在反比例函数的图象上时,
根据A'O'=AO=2,A'O'⊥x轴,可得直线AA'由直线OO'向下平移2个单位得到的,
∴直线AA'的解析式为y=x-2,
解方程组$\left\{\begin{array}{l}{y=x-2}\\{y=\frac{8}{x}}\end{array}\right.$,可得$\left\{\begin{array}{l}{x=4}\\{y=2}\end{array}\right.$,或$\left\{\begin{array}{l}{x=-2}\\{y=-4}\end{array}\right.$,
∴A“(4,2),A1(-2,-4),
又∵A(2,0),
∴线段AA“的中点坐标为(3,1),
把(3,1)代入直线y=-x+m,可得m=4,
∴当线段O′A′与反比例函数y=$\frac{8}{x}$(x>0)恰有一个公共点时,2$\sqrt{2}$≤m≤4;
同理,把线段OO2的中点坐标(-$\sqrt{2}$,-$\sqrt{2}$)代入直线y=-x+m,可得m=-2$\sqrt{2}$,
把线段AA1的中点坐标(0,-2)代入直线y=-x+m,可得m=-2,
∴当线段O′A′与反比例函数y=$\frac{8}{x}$(x<0)恰有一个公共点时,-2$\sqrt{2}$≤m≤-2;
综上所述,m的取值范围为2$\sqrt{2}$≤m≤4或-2$\sqrt{2}$≤m≤-2.
点评 本题主要考查了反比例函数与一次函数交点问题以及一次函数图象与几何变换的运用,解决问题的关键是运用分类讨论的思想,画出图形进行分析.解题时注意:直线y=-x+m与直线y=x互相垂直.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
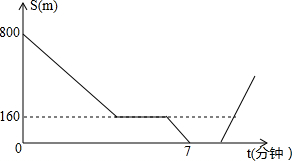 在一次集训中,一支队伍出发10分钟后,通讯员骑自行车追上队尾传达命令,然后按原速到队首传达命令后继续按原速原路返回.在此过程中队伍一直保持匀速行进,如图所示是通讯员与队首的距离S(米)和通讯员所用时间t(分钟)之间的函数图象.若传达命令所花时间都为2分钟,则当通讯员再次回到队尾时,他一共走了1560米.
在一次集训中,一支队伍出发10分钟后,通讯员骑自行车追上队尾传达命令,然后按原速到队首传达命令后继续按原速原路返回.在此过程中队伍一直保持匀速行进,如图所示是通讯员与队首的距离S(米)和通讯员所用时间t(分钟)之间的函数图象.若传达命令所花时间都为2分钟,则当通讯员再次回到队尾时,他一共走了1560米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
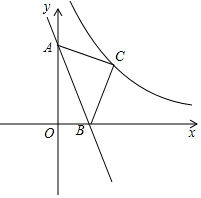 如图,在平面直角坐标系中,将直线y=-3x向上平移3个单位,与y轴、x轴分别交于点A、B,以线段AB为斜边在第一象限内作等腰直角三角形ABC.若反比例函数y=$\frac{k}{x}$(x>0)的图象经过点C,求此反比例函数的表达式.
如图,在平面直角坐标系中,将直线y=-3x向上平移3个单位,与y轴、x轴分别交于点A、B,以线段AB为斜边在第一象限内作等腰直角三角形ABC.若反比例函数y=$\frac{k}{x}$(x>0)的图象经过点C,求此反比例函数的表达式.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
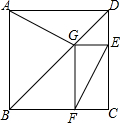 如图为某城市部分街道示意图,四边形ABCD为正方形,点G在对角线BD上,GE⊥CD,GF⊥BC,AD=1500m,小敏行走的路线为B→A→G→E,小聪行走的路线为B→A→D→E→F.若小敏行走的路程为3100m,则小聪行走的路程为4600m.
如图为某城市部分街道示意图,四边形ABCD为正方形,点G在对角线BD上,GE⊥CD,GF⊥BC,AD=1500m,小敏行走的路线为B→A→G→E,小聪行走的路线为B→A→D→E→F.若小敏行走的路程为3100m,则小聪行走的路程为4600m.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com