
(本题满分10分,每小题5分)
如图,AB为⊙O的直径,弦CD⊥AB,垂足为点M,AE切⊙O于点A,交BC的延长线于点E,连接AC.
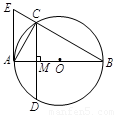
(1)若∠B=30°,AB=2,求CD的长;
(2)求证:AE2=EB·EC.
(1)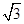
(2)证明略
【解析】
解:(1)解法一: 解法二:
∵AB为⊙O的直径, ∵AB为⊙O的直径,∠B=30°,
∴∠ACB=90°.……1分
∴AC=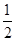 AB=1,BC=AB•cos30°=
AB=1,BC=AB•cos30°=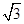 …2分
…2分
∵在Rt△ABC中,∠B=30°,AB=2, ∵弦CD⊥直径AB于点M,
∴BC=AB•cos30°=2×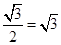 …2分
∴CD=2CM,AB×CM=AC×BC……4分
…2分
∴CD=2CM,AB×CM=AC×BC……4分
∵弦CD⊥直径AB,∠B=30°,
∴CD=2CM=2×
∴ CM=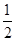 BC=
BC=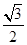 .……4分
=2×
.……4分
=2× =
=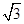 ……5分
……5分
CD=2CM=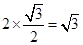 .……5分
.……5分
(其它解法请酌情给分)
(2)证明:∵AE切⊙O于点A,AB为⊙O的直径,
∴∠BAE=90°,∠ACE=∠ACB=90°, 6分
∴∠ACE=∠BAE=90°. 7分
又∵∠E=∠E,
∴Rt△ECA∽Rt△EAB. 8分
∴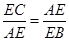 . 9分
. 9分
∴AE2=EB•EC. 10分


科目:初中数学 来源: 题型:
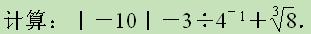
查看答案和解析>>
科目:初中数学 来源:2010--2011学年度山东潍坊市四县市七年级第二学期期末质量监测数学 题型:解答题
(本题满分10分,每小题5分)
(1)(11·贺州)(本题满分5分)

(2)(11·贺州)(本题满分5分)先化简,再求值:(a+1) (a-1)+a (1-a),其中a=2012.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com