

���� ��1����������֤��CAD�ա�BAE���Ӷ���CD=BE����ACD=��ABE������������������ʺ��ڽǺͶ����Ϳ������CBE=90�㣬�Ӷ��õ�CD��BE��
��2�������1����֤��˼·�Ϳɵõ�CD��BE��Ȼ������
��3���ӳ�CD��BE�ڵ�F����AB��O����ͼ�ܣ������2����֤��˼·���ɽ�����⣮
��4���ӳ�CD��BE�ڵ�F����AB��O����ͼ�ݣ������3����֤��˼·���ɽ�����⣮
��� �⣺��1����ͼ�ڣ�
�ߡ�CAB=��DAE=90�㣬
���CAD=��BAE��
�ڡ�CAD�͡�BAE�У�
$\left\{\begin{array}{l}{AC=AB}\\{��CAD=��BAE}\\{AD=AE}\end{array}\right.$��
���CAD�ա�BAE��SAS����
��CD=BE����ACD=��ABE��
���CBE=��CBA+��ABE=��CBA+��ACD=180��-��CAB
�ߡ�CAB=90�㣬
���CBE=180��-90��=90�㼴CD��BE��
��2������D��CB���ӳ�����ʱ����ͼ�ۣ�
ͬ���ɵã���CBE=90�㼴CD��BE��
�ʴ�Ϊ��CD��BE��
��3������D�ڡ�ABC��ʱ��CD��BE��Ȼ������
֤������ͼ�ܣ�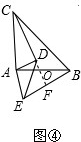
�ӳ�CD��BE�ڵ�F����AB��O��
ͬ���ɵã���ACD=��ABE��
�ߡ�C0B=��ACO+��CAO=��ABE+��OFB��
���CAO=��OFB��
�ߡ�CAO=90�㣬
���OFB=90�㣬��CD��BE��
��4���ӳ�CD��BE�ڵ�F����AB��O����ͼ�ݣ�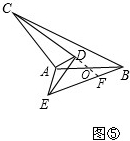
�ɣ�3���á�CAO=��OFB��
�ߡ�CAB=x�㣬
���OFB=x�㣮
���CFE=180��-x�㣮
��90�㣼x�㣼180�㣬
��0��180��-x�㣼90�㣮
��ֱ��CD��ֱ��BE�ཻ���ɵ����Ϊ180��-x�㣮
�ʴ�Ϊ��180��-x�㣮
���� ���⿼����ȫ�������ε��ж������ʡ����������ε����ʡ������ε�������ʡ������ε��ڽǺͶ�����֪ʶ�����������������н��⾭�����������������������ȵ��������������ζ��Ƕ����غϣ����Ȼ�����ȫ�������Σ�������һ�������ο�������һ�����������Ŷ��Ƕ�����ת���ã����ǰ����ֻ���ģ�ͳ�Ϊ��תȫ���ͣ���Ϥ����ģ�Ϳ�����߽����ٶȣ�Ӧ���ӶԻ���ģ�͵Ļ��ۣ�


 ������ѧ���̲���ȫ���ϵ�д�
������ѧ���̲���ȫ���ϵ�д� ������ʱ����ҵ����ϵ�д�
������ʱ����ҵ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1��2 | B�� | 2��1 | C�� | 1��4 | D�� | 1��5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ��ʾ����ֻ�ֵ�ʳָ��Ĵָ��ͬһƽ���ڣ����ǹ��ɵ�һ�Խǿ��Կ��ɣ�������
��ͼ��ʾ����ֻ�ֵ�ʳָ��Ĵָ��ͬһƽ���ڣ����ǹ��ɵ�һ�Խǿ��Կ��ɣ�������| A�� | �ڴ��� | B�� | ͬλ�� | C�� | ͬ���ڽ� | D�� | �Զ��� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | sin��-1 | B�� | -sin��-1 | C�� | 1-sin�� | D�� | ��ȷ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\root{3}{7}$$��2��\sqrt{5}$ | B�� | 2$��\root{3}{7}$$��\sqrt{5}$ | C�� | 2$��\sqrt{5}$$��\root{3}{7}$ | D�� | $\sqrt{5}$$��\root{3}{7}$��2 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com