已知一次函数y=-2x+2与x轴、y轴分别交于A、B点,以AB为边在第一象限内作直角△ABC,△ABC∽△OAB.
(1)求点C的坐标;
(2)一个反比例函数的图象经过不同的点C和点P,问:在第一象限内,是否存在点P(记点P的横坐标为m)使得△PAB的面积等于△ABC的面积?若存在,请求出点P的坐标;若不存在,请说明理由.
分析:(1)先求点B、A的坐标,由勾股定理得,AB=
,由△ABC∽△OAB,可得点C(5,2);
(2)存在,由(1)可知AB=
,AC=2
,再求出△ABC的面积,设这个反比例函数关系式为
y=(k≠0).
求得解析式,再直线CP的解析式为y=kx+b,求出解析式,由S
△PAB=S
△DOE-S
△PBE-S
△AOB-S
△PAD,求出m,从而求出点P的坐标为(1,10).
解答:解:(1)当x=0时,y=2,则点B(0,2);
当y=0时,解得x=1,则点A(1,0)
∵在直角△ABC中,AO=1,BO=2,∴AB=
=
,
∵△ABC∽△OAB,∴
=
=
=
,
解得AC=2
,BC=5,
∵△ABC∽△OAB,∴∠ABC=∠BAO,
∴∠OBC=∠OBA+∠ABC=∠OBA+∠BAO=90°,
∴点C(5,2);
(2)存在
∵由(1)可知AB=
,AC=2
,
∴△ABC的面积=
AB•AC=5
设这个反比例函数关系式为
y=(k≠0).
∵反比例函数的图象经过点C(5,2),∴k=10,
∴y=
.
∵点P是反比例函数y=
图象上,且在第一象限内的点,
∴可设点P的坐标为(m,
),m>0且m≠5(5分)
设直线CP的解析式为y=kx+b,∵C(5,2),P(m,
),
∴
解得
∴
y=-x+(m>0且m≠5).
当x=0时,
y=,当y=0时,x=5+m.
设直线CP与x轴、y轴分别交于D、E点,则OD=5+m,OE=
∵S
△PAB=S
△DOE-S
△PBE-S
△AOB-S
△PAD=
(5+m)
-
•m•
-
×1×2-
(4+m)•
=m+
-1
=5
∴解得m=1或m=5
∵m>0,且m≠5
∴m=1
∴点P的坐标为(1,10)
点评:此题作为压轴题,综合考查函数、方程与勾股定理,三角形相似的判定与性质等知识.
此题是一个大综合题,难度较大,有利于培养同学们的钻研精神和坚韧不拔的意志品质.



 名校课堂系列答案
名校课堂系列答案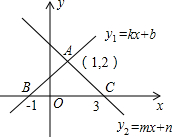 如图所示,已知一次函数y1=kx+b的图象经过A(1,2)、B(-1,0)两点,y2=mx+n的图象经过A、C(3,0)两点,则不等式组0<kx+b<mx+n的解集是( )
如图所示,已知一次函数y1=kx+b的图象经过A(1,2)、B(-1,0)两点,y2=mx+n的图象经过A、C(3,0)两点,则不等式组0<kx+b<mx+n的解集是( )