练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    解放桥是天津市的标志性建筑之一，是一座全钢结构的部分可开启的桥梁．

    （Ⅰ）如图①，已知解放桥可开启部分的桥面的跨度AB等于47m，从AB的中点C处开启，则AC开启至A′C′的位置时，A′C′的长为　 　m；

    （Ⅱ）如图②，某校数学兴趣小组要测量解放桥的全长PQ，在观景平台M处测得∠PMQ=54°，沿河岸MQ前行，在观景平台N处测得∠PNQ=73°，已知PQ⊥MQ，MN=40m，求解放桥的全长PQ（tan54°≈1.4，tan73°≈3.3，结果保留整数）．


                  解：（I）∵点C是AB的中点，

    ∴A'C'=AB=23.5m．

    （II）设PQ=x，

    在Rt△PMQ中，tan∠PMQ==1.4，

    ∴MQ=，

    在Rt△PNQ中，tan∠PNQ==3.3，

    ∴NQ=，

    ∵MN=MQ﹣NQ=40，即﹣=40，

    解得：x≈97．

    答：解放桥的全长约为97m．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    如图，已知在△ABC中，AB=AC，以AB为直径的⊙O与边BC交于点D，与边AC交于点E，过点D作DF⊥AC于F．

    （1）求证：DF为⊙O的切线；

    （2）若DE=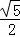，AB=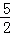，求AE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    在Rt△ABC中，∠ACB=90°，CD是斜边AB上的中线，CD=4，AC=6，则sinB的值是　　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，△ABC的项点都在正方形网格的格点上，则cosC的值为（　　）

    A．           B．          C．           D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在地面上的点A处测得树顶B的仰角为α度，AC=7米，则树高BC为　　 米（用含α的代数式表示）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


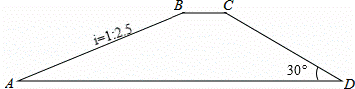
    如图，一水库大坝的横断面为梯形ABCD，坝顶BC宽6米，坝高20米，斜坡AB的坡度i=1：2.5，斜坡CD的坡角为30°，求坝底AD的长度．（精确到0.1米，参考数据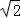：≈1.414，≈1.732．提示：坡度等于坡面的铅垂高度与水平长度之比）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，将边长为4个单位的等边△ABC沿边BC向右平移2个单位得到△DEF，则四边形ABFD的周长为（　　）

    A．  12            B．16            C．20            D． 24

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，将矩形ABCD沿对角线AC剪开，再把△ACD沿CA方向平移得到△A′C′D′．

    （1）证明△A′AD′≌△CC′B；

    （2）若∠ACB=30°，试问当点C'在线段AC上的什么位置时，四边形ABC′D′是菱形，并请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


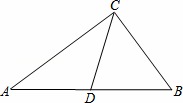
    如图，在Rt△ABC中，∠ACB=90°，AC=4，BC=3，点D为AB的中点，将△ACD绕着点C逆时针旋转，使点A落在CB的延长线A′处，点D落在点D′处，则D′B长为　　．

    查看答案和解析>>

    同步练习册答案