
【题目】某校七年级社会实践小组去某商场调查商品的销售情况,了解到该商场以每件80元的价格购进了某品牌衬衫500件,并以每件120元的价格销售了400件,商场准备采取促销措施,将剩下的衬衫降价销售.
(1)每件衬衫降价多少元时,销售完这批衬衫正好达到盈利45%的预期目标?
(2)某公司给员工发福利,在该商场促销钱购买了20件该品牌的衬衫发给员工,后因为有新员工加入,又要购买5件该衬衫,购买这5件衬衫时恰好赶上该商场进行促销活动,求该公司购买这25件衬衫的平均价格.
科目:初中数学 来源: 题型:
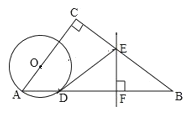
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 在
在![]() 上,以
上,以![]() 为半径的
为半径的![]() 交
交![]() 于点
于点![]() ,
,![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .
.
(1)判断直线![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)若![]() ,
,![]() ,
,![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】规定两数a,b之间的一种运算,记作(a,b):如果![]()
![]() ,那么(a,b)=c.
,那么(a,b)=c.
例如:因为23=8,所以(2,8)=3.
(1)根据上述规定,填空:
(3,27)=_______,(5,1)=_______,(2,![]()
![]() )=_______.
)=_______.
(2)小明在研究这种运算时发现一个现象:(3n,4n)=(3,4)小明给出了如下的证明:
设(3n,4n)=x,则(3n)x=4n,即(3x)n=4n
所以3x=4,即(3,4)=x,
所以(3n,4n)=(3,4).
请你尝试运用这种方法证明下面这个等式:(3,4)+(3,5)=(3,20)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2h,并且甲车途中休息了0.5h,如图是甲乙两车行驶的距离y(km)与时间x(h)的函数图象.则下列结论:
(1)a=40,m=1;
(2)乙的速度是80km/h;
(3)甲比乙迟![]() h到达B地;
h到达B地;
(4)乙车行驶![]() 小时或
小时或![]() 小时,两车恰好相距50km.
小时,两车恰好相距50km.
正确的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
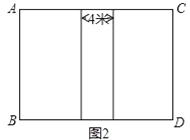
【题目】某校为学生开展拓展性课程,拟在一块长比宽多6米的长方形场地内建造由两个大棚组成的植物养殖区(如图1),要求两个大棚之间有间隔4米的路,设计方案如图2,已知每个大棚的周长为44米.
(1)求每个大棚的长和宽各是多少?
(2)现有两种大棚造价的方案,方案一是每平方米60元,超过100平方米优惠500元,方案二是每平方米70元,超过100平方米优惠总价的20%,试问选择哪种方案更优惠?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现计划把一批货物用一列火车运往某地![]() 已知这列火车可挂A,B两种不同规格的货车厢共40节,使用A型车厢每节费用6000元,使用B型车厢每节费用为8000元.
已知这列火车可挂A,B两种不同规格的货车厢共40节,使用A型车厢每节费用6000元,使用B型车厢每节费用为8000元.
![]() 设运送这批货物的总费用为y元,这列火车挂A型车厢x节,写出y关于x的函数表达式,并求出自变量x的取值范围;
设运送这批货物的总费用为y元,这列火车挂A型车厢x节,写出y关于x的函数表达式,并求出自变量x的取值范围;
![]() 已知A型车厢数不少于B型车厢数,运输总费用不低于276000元,问有哪些不同运送方案?
已知A型车厢数不少于B型车厢数,运输总费用不低于276000元,问有哪些不同运送方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l和双曲线 ![]() 交于A,B两点,P是线段AB上的点(不与A,B重合),过点A,B,P分别向x轴作垂线,垂足分别为C,D,E,连接OA,OB,0P,设△AOC的面积为S1、△BOD的面积为S2、△POE的面积为S3 , 则( )
交于A,B两点,P是线段AB上的点(不与A,B重合),过点A,B,P分别向x轴作垂线,垂足分别为C,D,E,连接OA,OB,0P,设△AOC的面积为S1、△BOD的面积为S2、△POE的面积为S3 , 则( )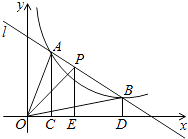
A.S1<S2<S3
B.S1>S2>S3
C.S1=S2>S3
D.S1=S2<S3
查看答案和解析>>
科目:初中数学 来源: 题型:
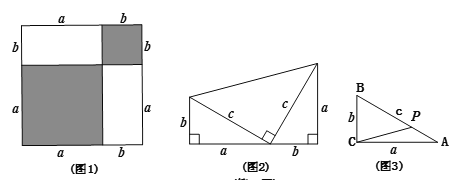
【题目】(1)用不同的方法计算如图中阴影部分的面积得到的等式: ;
(2)如图是两个边长分别为![]() 、
、![]() 、
、![]() 的直角三角形和一个两条直角边都是
的直角三角形和一个两条直角边都是![]() 的直角三角形拼成,试用不同的方法计算这个图形的面积,你能发现什么?说明理由;
的直角三角形拼成,试用不同的方法计算这个图形的面积,你能发现什么?说明理由;
(3)根据上面两个结论,解决下面问题:若如图中,直角![]() 三边a、
三边a、![]() 、c,
、c,
①满足![]() ,ab=18,求
,ab=18,求![]() 的值;
的值;
②在①的条件下,若点![]() 是边
是边![]() 上的动点,连接
上的动点,连接![]() ,求线段
,求线段![]() 的最小值;
的最小值;
③若![]() ,
,![]() ,且
,且![]() ,则
,则![]() 的值是 .
的值是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com