
 如图,在△ABC中,D是AB的中点,E是BC上的一点,且BE=4EC,CD与AE相交于点F,若△CEF的面积为1,则△ABC的面积为( )
如图,在△ABC中,D是AB的中点,E是BC上的一点,且BE=4EC,CD与AE相交于点F,若△CEF的面积为1,则△ABC的面积为( )| A. | 24 | B. | 25 | C. | 30 | D. | 32 |
分析 解法一:作辅助线,构建平行线,利用三角形中位线定理得:DG=$\frac{1}{2}$BE,与已知BE=4EC相结合得出DG与EC的比,因为△DGF∽△CEF,根据面积比等于相似比的平方可知S△DFG=4,可依次得出△DFE、△DEC、△BDE、△BDC的面积,由此得出结论.
解法二:如图2,作辅助线,利用同高三角形面积的比就是对应底边的比得:S△BEF=4S△EFC=4,证明△DGF∽△CEF,则$\frac{DF}{FC}=\frac{DG}{EC}=2$,求S△BDF=2S△BFC=10,最后根据三角形中线平分面积的性质得结论.
解答 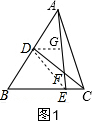 解:解法一:如图1,过D作DG∥BC,交AE于G,则△DGF∽△CEF,
解:解法一:如图1,过D作DG∥BC,交AE于G,则△DGF∽△CEF,
∵AD=BD,
∴AG=GE,
∴DG=$\frac{1}{2}$BE,
∵BE=4EC,
∴$\frac{DG}{EC}$=2,
∵△DGF∽△CEF,
∴$\frac{{S}_{△DFG}}{{S}_{△CEF}}$=4,$\frac{GF}{FE}=\frac{DG}{EC}$=2,
∵S△CEF=1,
∴S△DFG=4,
∴${S}_{△DFE}=\frac{1}{2}{S}_{△DFG}$=2,
∴S△DEC=S△DFE+S△CEF=2+1=3,
∴S△BDE=4S△DEC=4×3=12,
∴S△BDC=S△BDE+S△DEC=12+3=15,
∴S△ABC=2S△BDC=2×15=30.
解法二:如图2,连接BF,
∵BE=4EC,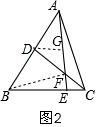
∴S△BEF=4S△EFC=4,
在AE上取中点G,连接DG,
∵D是AB的中点,
∴DG是△ABE的中位线,
∴DG=$\frac{1}{2}$BE,
∵BE=4EC,
∴DG=2EC,
∵DG∥EC,
∴△DGF∽△CEF,
∴$\frac{DF}{FC}=\frac{DG}{EC}=2$,
∴S△BDF=2S△BFC=2(S△BEF+S△EFC)=2×(4+1)=10,
∴S△BDC=10+5=15,
∵D是AB的中点,
∴S△ABC=2S△BDC=30,
或连接BF.∵BE=4EC,且S△CEF=1,∴S△BEF=4;∵点D是AB中点,∴S△BDF=S△ADF=x,S△BDC=S△ADC;即S△AFC+x=x+5,∴S△AFC=5,因为S△CEF1,所以S△AEC=6,又因为BE=4EC,所以S△ABE=24,所以S△ABC=30
故选C.
点评 本题是三角形的面积问题,考查了三角形面积与底和高的关系,做好本题要知道以下内容:①两个同高的三角形的面积的比等于对应底的比;②平行于三角形一边的直线必平分第三边;③三角形的中线将三角形分成了两个面积相等的三角形;④相似三角形面积的比等于相似比的平方.


 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 李欣同学调查了班里同学在上学期内购买课外书的花费情况,并将结果绘制成了下面的统计图.
李欣同学调查了班里同学在上学期内购买课外书的花费情况,并将结果绘制成了下面的统计图.查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 八年级(3)班全体女生 | B. | 该校全体女生 | ||
| C. | 八年级(3)班全体学生 | D. | 该校全体学生 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 6,(-3,5) | B. | 10,(3,-5) | C. | 1,(3,4) | D. | 3,(3,2) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com