
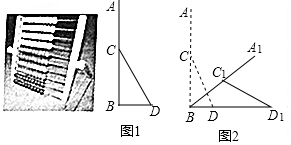
分析 首先利用勾股定理得出BD的长,再过点C1作C1H⊥BD1于点H,进而得出BH=10$\sqrt{3}$cm,求出∠ABC1=60°,利用弧长公式求出点A经过的路径的长,再求出D1C1=25cm,C1H=10cm,进而得出D1H、BD1的长,即可得出答案.
解答 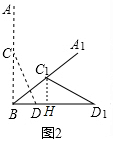 解:∵AB=40,点C是AB的中点,
解:∵AB=40,点C是AB的中点,
∴BC=$\frac{1}{2}$AB=20cm,
∵AB⊥BD,
∴∠CBD=90°,
在Rt△BCD中,BC=20cm,DC=25cm,
∴BD=$\sqrt{C{D}^{2}-C{B}^{2}}$=$\sqrt{2{5}^{2}-2{0}^{2}}$=15(cm),
过点C1作C1H⊥BD1于点H,
则∠C1HD=C1HD1=90°,
在Rt△BC1H中,BC1=20cm,C1H=10cm,
∴∠C1BH=30°,故BH=10$\sqrt{3}$cm,
则∠ABC1=60°,
故点A经过的路径的长为:$\frac{60π×40}{180}$=$\frac{40π}{3}$≈42(m),
在Rt△D1C1H中,D1C1=25cm,C1H=10cm,
∴D1H=$\sqrt{{{C}_{1}D}_{1}^{2}-{C}_{1}{H}^{2}}$=$\sqrt{2{5}^{2}-1{0}^{2}}$=5$\sqrt{21}$(cm),
∴BD1=BH+HD1=10$\sqrt{3}$+5$\sqrt{21}$≈17.32+22.915=40.235(cm),
∴点D滑动的距离为:BD1-BD=40.235-15=25.235≈25(cm),
答:点D滑动的距离为25m,点A经过的路径的长为42m.
点评 此题主要考查了解直角三角形的应用以及勾股定理、弧长公式的应用,正确应用勾股定理是解题关键.


 优等生题库系列答案
优等生题库系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图是用完全相同的火柴棍拼成一排由三角形组成的图形示意图.若拼成的图形中有n个菱形,则需要火柴棍的根数是( )
如图是用完全相同的火柴棍拼成一排由三角形组成的图形示意图.若拼成的图形中有n个菱形,则需要火柴棍的根数是( )| A. | n+4 | B. | 2n+1 | C. | 2n+3 | D. | 4n+1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
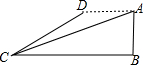 如图,飞机的高度AB=1000千米,从飞机上测得地面着陆点C的俯角为18°,飞机水平飞行一段距离后,到达D点,此时测得地面着陆点C的俯角为30°,求飞机飞行的距离AD的长(参考数据:$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41,tan18°≈0.32)
如图,飞机的高度AB=1000千米,从飞机上测得地面着陆点C的俯角为18°,飞机水平飞行一段距离后,到达D点,此时测得地面着陆点C的俯角为30°,求飞机飞行的距离AD的长(参考数据:$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41,tan18°≈0.32)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com