
【题目】如图,已知![]() 为等边三角形,点
为等边三角形,点![]() 由点
由点![]() 出发,在
出发,在![]() 延长线上运动,连接
延长线上运动,连接![]() ,以
,以![]() 为边作等边三角形
为边作等边三角形![]() ,连接
,连接![]() .
.
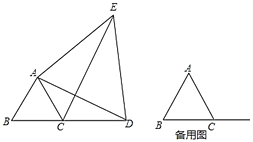
(1)证明:![]() ;
;
(2)若![]() ,点
,点![]() 的运动速度为每秒
的运动速度为每秒![]() ,运动时间为
,运动时间为![]() 秒,则
秒,则![]() 为何值时,
为何值时,![]() ?
?
【答案】(1)证明过程见解析;(2)3.
【解析】
(1)根据等腰三角形的性质得出AB=AC=BC、AD=AE、∠BAC=∠DAE,再根据角的等量代换即可证出△BAD≌△CAE,即可得出答案;
(2)根据等边三角形的性质得出CE是△ADE的边AD的垂直平分线,即可得出答案.
(1)证明:∵△ABC和△ADE均为等边三角形
∴AB=AC=BC,AD=AE,∠BAC=60°,∠DAE=60°
∴∠BAC+∠CAD=∠DAE+∠CAD
即∠BAD=∠CAE
在△BAD和△CAE中
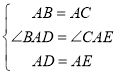
∴△BAD≌△CAE(SAS)
∴CE=BD
又BD=BC+CD=AC+CD
∴CE=AC+CD
(2)解:如图所示
∵△ADE是等边三角形
若CE⊥AD
则CE是△ADE的边AD的垂直平分线
∴CD=CA=AB=6
∴t=6÷2=3(s)


 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,AB=18,BC=12,∠DAB=60°,E在AB上,且AE:EB=1:2,F是BC的中点,过D分别作DP⊥AF于P,DQ⊥CE于Q,则下列结论正确的个数是( )
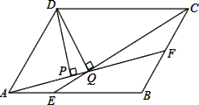
(1)CE平分∠BCD;(2)AF=CE;(3)连接DE、DF,则![]() ;(4)DP:DQ=
;(4)DP:DQ=![]()
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,则在下列各式子:①abc>0;②a+b+c>0;③a+c>b;④2a+b=0;⑤![]() =b2-4ac<0中,成立的式子有( )
=b2-4ac<0中,成立的式子有( )
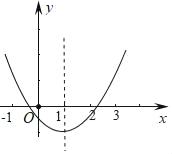
A. ②④⑤ B. ②③⑤
C. ①②④ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=90°,BC=8 AB=6cm,动点P从点A开始沿边AB向点B以1cm/s的速度移动,动点Q从点B开始沿边BC向点C以2cm/s的速度移动.若P,Q两点分别从A,B两点同时出发,在运动过程中,△PBQ的最大面积是( )
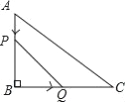
A. 18cm2 B. 12cm2 C. 9cm2 D. 3cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中考英语听力测试期间T需要杜绝考点周围的噪音.如图,点A是某市一中考考点,在位于考点南偏西15°方向距离500米的C点处有一消防队.在听力考试期间,消防队突然接到报警电话,消防车需沿北偏东75°方向的公路CF前往救援.已知消防车的警报声传播半径为400米,若消防车的警报声对听力测试造成影响,则消防车必须改道行驶.试问:消防车是否需要改道行驶?
说明理由.(![]() ≈1.732)
≈1.732)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方体的长为15,宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是__________

查看答案和解析>>
科目:初中数学 来源: 题型:
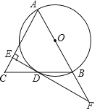
【题目】如图,![]() 是
是![]() 的直径,
的直径,![]() 是
是![]() 的弦,延长
的弦,延长![]() 到点
到点![]() ,使
,使![]() ,连结
,连结![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,交
,交![]() 的延长线于点
的延长线于点![]() .
.
![]() 求证:
求证:![]() 为
为![]() 的切线;
的切线;
![]() 猜想线段
猜想线段![]() 、
、![]() 、
、![]() 之间的数量关系,并证明你的猜想;
之间的数量关系,并证明你的猜想;
![]() 若
若![]() ,
,![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
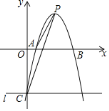
【题目】如图,在平面直角坐标系中,二次函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,其顶点为
,其顶点为![]() ,连接
,连接![]() 、
、![]() 、
、![]() ,过点
,过点![]() 作
作![]() 轴的垂线
轴的垂线![]() .
.
(1)求点![]() ,
,![]() 的坐标;
的坐标;
(2)直线![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 的面积等于
的面积等于![]() 的面积的
的面积的![]() 倍?若存在,求出点
倍?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com