
| A. | 图象在第一、三象限 | B. | 图象经过点(2,-8) | ||
| C. | 当x>0时,y随x的增大而减小 | D. | 当x<0时,y随x的增大而增大 |
分析 反比例函数y=$\frac{k}{x}$(k≠0)中的k<0时位于第二、四象限,在每个象限内,y随x的增大而增大;在不同象限内,y随x的增大而增大,根据这个性质选择则可.
解答 解:A、因为k=-4<0,所以函数图象位于二、四象限,故本选项错误;
B、因为k=-4≠-8×2,所以图象不过点(2,-8),故本选项错误;
C、因为k=-4<0,所以函数图象位于二、四象限,在每一象限内y随x的增大而增大,故本选项错误;
D、因为k=-4<0,所以函数图象位于二、四象限,在每一象限内y随x的增大而增大,故本选项正确;
故选D.
点评 本题考查了反比例函数图象的性质:
①当k>0时,图象分别位于第一、三象限;当k<0时,图象分别位于第二、四象限.
②当k>0时,在同一个象限内,y随x的增大而减小;当k<0时,在同一个象限,y随x的增大而增大.注意反比例函数的图象应分在同一象限和不在同一象限两种情况分析.


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:解答题
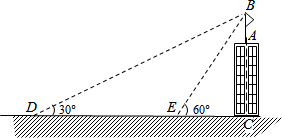 如图,某建筑物AC顶部有一旗杆AB,且点A,B,C在同一条直线上,小明在地面D处观测旗杆顶端B的仰角为30°,然后他正对建筑物的方向前进了20米到达地面的E处,又测得旗杆顶端B的仰角为60°,已知建筑物的高度AC=12m,求旗杆AB的高度(结果精确到0.1米).参考数据:$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41.
如图,某建筑物AC顶部有一旗杆AB,且点A,B,C在同一条直线上,小明在地面D处观测旗杆顶端B的仰角为30°,然后他正对建筑物的方向前进了20米到达地面的E处,又测得旗杆顶端B的仰角为60°,已知建筑物的高度AC=12m,求旗杆AB的高度(结果精确到0.1米).参考数据:$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | P1=P2 | B. | P1>P2 | C. | P1<P2 | D. | P1≤P2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 18个 | B. | 28个 | C. | 36个 | D. | 42个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,四边形OABC是平行四边形,对角线OB在y轴正半轴上,位于第一象限的点A和第二象限的点C分别在双曲线y=$\frac{{k}_{1}}{x}$和y=$\frac{{k}_{2}}{x}$的一支上,分别过点A,C作x轴的垂线,垂足分别为M和N,则有以下结论:
如图,四边形OABC是平行四边形,对角线OB在y轴正半轴上,位于第一象限的点A和第二象限的点C分别在双曲线y=$\frac{{k}_{1}}{x}$和y=$\frac{{k}_{2}}{x}$的一支上,分别过点A,C作x轴的垂线,垂足分别为M和N,则有以下结论:| A. | ①④ | B. | ①③ | C. | ①②④ | D. | ①③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
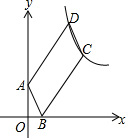 如图,在直角坐标系中,平行四边形ABCD的顶点A(0,2)、B(1,0)在x轴、y轴上,另两个顶点C、D在第一象限内,且AD=3AB.若反比例函数$y=\frac{k}{x}$(k>0)的图象经过C,D两点,则k的值是24.
如图,在直角坐标系中,平行四边形ABCD的顶点A(0,2)、B(1,0)在x轴、y轴上,另两个顶点C、D在第一象限内,且AD=3AB.若反比例函数$y=\frac{k}{x}$(k>0)的图象经过C,D两点,则k的值是24.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
| 摸到白球的次数m | 58 | 96 | 116 | 295 | 484 | 601 |
| 摸到白球的频率$\frac{m}{n}$ | 0.58 | 0.64 | 0.58 | 0.59 | 0.605 | 0.601 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com