
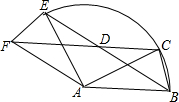
 如图,△ABC中,AB=AC=2,∠BAC=30°,△AEF是由△ABC绕点A按逆时针方向旋转得到的,连接BE、CF相交于点D,$\widehat{BE}$是点B旋转形成的弧.
如图,△ABC中,AB=AC=2,∠BAC=30°,△AEF是由△ABC绕点A按逆时针方向旋转得到的,连接BE、CF相交于点D,$\widehat{BE}$是点B旋转形成的弧.分析 (1)由旋转的性质得到AE=AF=AB=AC,再判断出△ABE≌△ACF;
(2)先由CF∥AB,得到∠ACF=30°,再求出∠BAC,然后用弧长公式计算即可.
解答 解:(1)由旋转得,AB=AE=AC=AF,∠BAC=∠EAF,
∴∠BAC=∠CAF,
在△ABE和△ACF中,
$\left\{\begin{array}{l}{AB=AC}\\{∠BAE=∠CAF}\\{AE=AF}\end{array}\right.$,
∴△ABE≌△ACF;
(2)由(1)有△ABE≌△ACF,
∴∠ACF=∠ABE
∵四边形ABDF是菱形,
∴CF∥AB,
∴∠ACF=∠BAC=∠ABE=30°,
∵AB=AE,
∴∠ABE=∠AEB=30°,
∴∠BAE=120°,
∴$\widehat{BE}$的长为$\frac{120×π×2}{180}$=$\frac{4}{3}$π.
点评 此题是旋转的性质题,主要考查了旋转的性质,平行线的性质,圆的性质,解本题的关键件是求出∠BAE.


科目:初中数学 来源: 题型:填空题
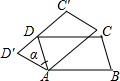 如图,在平行四边形ABCD中,∠BAD=110°,将四边形BCD绕点A逆时针旋转到平行四边形AB′C′D′的位置,旋转角α(0°<α<70°),若C′D′恰好经过点D,则α的度数为40°.
如图,在平行四边形ABCD中,∠BAD=110°,将四边形BCD绕点A逆时针旋转到平行四边形AB′C′D′的位置,旋转角α(0°<α<70°),若C′D′恰好经过点D,则α的度数为40°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在一次课外实践活动中,同学们要测量某公园人工湖两侧A,B两个凉亭之间的距离.现测得AC=50m,BC=100m,∠CAB=120°,请计算A,B两个凉亭之间的距离.
在一次课外实践活动中,同学们要测量某公园人工湖两侧A,B两个凉亭之间的距离.现测得AC=50m,BC=100m,∠CAB=120°,请计算A,B两个凉亭之间的距离.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com