
分析 首先根据题意作出图形,然后利用圆锥的有关计算公式进行计算即可.
解答 解:做法:
(1)通过分析、比较确定符合条件的扇形、圆与正方形的位置关系,并画出示意图,如图所示.
(2)通过它们的位置关系计算出扇形和圆的半径,并根据计算结果在纸片上画出截剪线.
(3)剪下符合条件的扇形与圆,用扇形作侧面,圆作底面粘接成圆锥.

其表面积的计算过程是:
如上图所示,设扇形的半径为Rcm,⊙O的半径为r cm,M、N均为切点,
连接OM、ON.则有OM⊥BC,ON⊥DC.
∵OM=ON=r.
∴四边形OMCN为正方形.
∴OC=$\sqrt{2}$r.
∵AC=AG+GO+OC,AC=$\sqrt{2}$AB=20$\sqrt{2}$cm,
∴R+r+$\sqrt{2}$r=20$\sqrt{2}$. ①
∵$\widehat{EF}$的弧长等于⊙O的周长,
∴$\frac{1}{4}$×2πR=2πr,即R=4r. ②
由①②得r=$\frac{20\sqrt{2}}{5+\sqrt{2}}$≈4.41,
∴S表=S扇+S底=$\frac{1}{4}$πR2+πr2=5πr2=5×3.14×4.412≈305cm2.
故所做圆锥的表面积约为305.3cm2.
点评 考查了圆锥的计算,解题的关键是能够作出图形并利用有关公式进行正确的计算,难度不大.


科目:初中数学 来源: 题型:解答题
 如图,在四边形ABFC中,∠BAC=∠BFC=∠BCN=90°,E为BC中点,过C作CN⊥BC交AF于N点,连接EN交BF于M点,连接CM交AN于G点,若AB=AF,求证:MG=GC.
如图,在四边形ABFC中,∠BAC=∠BFC=∠BCN=90°,E为BC中点,过C作CN⊥BC交AF于N点,连接EN交BF于M点,连接CM交AN于G点,若AB=AF,求证:MG=GC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
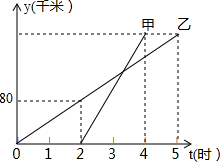 甲、乙两车沿相同路线以各自的速度从A地去往B地,如图表示其行驶过程中路程y(千米)随时间t(小时)的变化图象,下列说法:
甲、乙两车沿相同路线以各自的速度从A地去往B地,如图表示其行驶过程中路程y(千米)随时间t(小时)的变化图象,下列说法:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
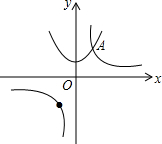 如图,抛物线y=x2+1与双曲线y=$\frac{k}{x}$的交点A的横坐标是1,则关于x的不等式$\frac{k}{x}<{x^2}$+1的解集是( )
如图,抛物线y=x2+1与双曲线y=$\frac{k}{x}$的交点A的横坐标是1,则关于x的不等式$\frac{k}{x}<{x^2}$+1的解集是( )| A. | x>1 | B. | x<0 | C. | 0<x<1 | D. | x<0或x>1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com