
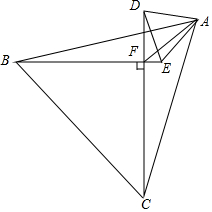
 正△ABC,正△ADE,BE⊥CD,F为垂足,AF=1,求S△ABC+S△ADE.
正△ABC,正△ADE,BE⊥CD,F为垂足,AF=1,求S△ABC+S△ADE. 分析 在AF右侧作等边△AFG,连接BD、CE、CG、FG、EG.首先证明△ABD≌△ACE(SAS),△ABD≌△ACE(SAS),△ADF≌△AEG(SAS),推出EG2+CG2=CE2,推出EG⊥CG,∠CGE=90°,再证明∠FCG=30°,∠FOG=60°,推出△FOG是等边三角形,根据S△ABC+S△ADE=$\frac{\sqrt{3}}{4}$×(BC2+DE2)计算即可.
解答 证明:在AF右侧作等边△AFG,连接BD、CE、CG、FG、EG.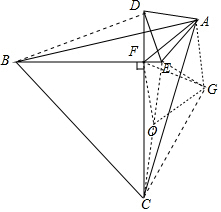
∵△ABC和△ADE是等边三角形,
∴AB=BC=AC,AD=AE=DE,∠BAD=∠CAE=60°-∠BAE,
∴△ABD≌△ACE(SAS),
∴BD=CE,
∵AF=AG=FG=1,∠BAF=∠CAG=60°-∠CAF,
∴△ABD≌△ACE(SAS),
∴BF=CG,∠ABF=∠ACG,
∵∠FAD=∠GAE=60°-∠EAF,
∴△ADF≌△AEG(SAS),
∴DF=EG,
∵BE⊥CD,
∴DF2+BF2=BD2,
∴EG2+CG2=CE2,
∴EG⊥CG,
∴∠CGE=90°
∵∠ABF+∠ACF=(∠ABC+∠ACB)-(∠FBC+∠FCB)=120°-90°=30°,
∴∠ACG+∠ACF=∠FCG=30°,
取CE的中点O,连接OF、OG.
∴OF=OC=OE=OG,
∴∠FOG=2∠FCG=60°,
∴△OFG是等边三角形,
∴CE=2FG=2,
∵EF2+DF2=DE2,BC2=BF2+CF2,
∴DE2+BC2=DE2+DF2+BF2+CF2=(DF2+BF2)+(EF2+CF2)=BD2+CE2=2CE2=8,
∴S△ABC+S△ADE=$\frac{\sqrt{3}}{4}$×(BC2+DE2)=$\frac{\sqrt{3}}{4}$×8=2√3.
点评 本题考查等边三角形的性质、全等三角形的判定和性质、勾股定理、直角三角形的判定和性质、直角三角形斜边中线定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,题目比较难,辅助线比较多.


 新思维寒假作业系列答案
新思维寒假作业系列答案科目:初中数学 来源: 题型:解答题
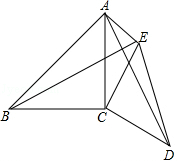 如图,已知∠ACB=∠DCE=90°,AC=BC,CD=CE
如图,已知∠ACB=∠DCE=90°,AC=BC,CD=CE查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -3 | B. | -2 | C. | -1 | D. | 0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com