Question

9．如图，已知抛物线与y轴交于点C（0，3），与x轴交于点A、B，点A在点B的左边，且B（3，0），AB=2
（1）求该抛物线的函数关系式；
（2）如果抛物线的对称轴上存在一点P，使得△APC的周长最小，求此时P点的坐标，并求出△APC周长；
（3）设D为抛物线上一点，E为对称轴上一点，若以点A、B、D、E为顶点的四边形是平行四边形，求点D的坐标．

Answer 1

分析 （1）先求出点A的坐标，根据两点式设出抛物线解析式，用待定系数法求出抛物线解析式；
（2）由点A，B关于抛物线对称轴对称，所以连接BC与抛物线对称轴的交点就是点P，根据两点间的距离公式求出各线段，即可；
（3）①AB为平行四边形的边时，就有AB∥DE，AB=DE，设出点D坐标，表示出点E坐标，由AB=DE求出点D坐标，
②AB为平行四边形的对角线时，AB，DE互相平分，而点E在抛物线对称轴上，得出点D也在抛物线对称轴上，即点D就是抛物线的顶点．

解答 解：（1）∵抛物线与x轴交于点A、B，点A在点B的左边，且B（3，0），AB=2，
∴A（1，0），
设抛物线解析式为y=a（x-1）（x-3），
∵点C在抛物线上，
∴3=a（-1）（-3）=3a，
∴a=1，
∴抛物线解析式为y=（x-1）（x-3）=x²-4x+3，
（2）如图1，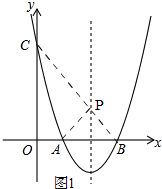

有（1）有，抛物线解析式为y=（x-1）（x-3）=x²-4x+3，
∴抛物线的对称轴为x=2，
连接BC，交对称轴于点P，连接AP，
∵点A与点B关于对称轴对称，
∴点P就是使得△APC的周长最小时，对称轴上的点，即：PA=PB，
∵B（3，0），C（0，3），
∴直线BC解析式为y=-x+3，BC=3$\sqrt{2}$，
当x=2时，y=1，
∵P（2，1），
∵A（1，0），C（0，3）
∴AC=$\sqrt{10}$，
∴△APC周长=AC+AP+CP=AC+BC=$\sqrt{10}$+3$\sqrt{2}$，
即：点P（2，1）时，△APC的周长最小，最小值为$\sqrt{10}$+3$\sqrt{2}$；
（3）∵以点A、B、D、E为顶点的四边形是平行四边形，
∴分AB为对角线和边两种情况计算，
①当AB为平行四边形的边时，AB∥DE，AB=DE，
∵点D在抛物线上，
∴设点D（m，m²-4m+3），
∵点E在抛物线对称轴x=2上，
∴点E（2，m²-4m+3），
∵DE∥AB，
∴DE=|m-2|，
∵AB=DE，AB=2，
∴|m-2|=2，
∴m=0，或m=4，
∴D（0，3）或（4，3），
②当AB为平行四边形的对角线时，AB与DE互相平分，
∵点E在抛物线对称轴上，
∴点D也在抛物线的对称轴上，
即：点D就是抛物线的顶点，
由（1）得，抛物线解析式为y=（x-1）（x-3），
∴抛物线顶点坐标为（2，-1），
∴满足条件的点D的坐标为（0，3）或（4，3）或（2，-1）．

点评 此题是二次函数综合题，主要考查了待定系数法，对称性，极值的确定，平行四边形的性质，解本题的关键是求出抛物线解析式，难点是分类讨论的思想和点P的坐标的确定．