

分析 (1)①根据OA=4,OC=2,可得点B的坐标;
②利用相似三角形的判定和性质得出点的坐标;
(2)根据平行四边形的性质,且分点在线段EF的延长线和线段上两种情况进行分析解答.
解答 解:(1)∵OA=4,OC=2,
∴点B的坐标为(4,2);
②如图1,过点P作PD⊥OA,垂足为点D,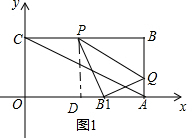
∵BQ:BP=1:2,点B关于PQ的对称点为B1,
∴B1Q:B1P=1:2,
∵∠PDB1=∠PB1Q=∠B1AQ=90°,
∴∠PB1D=∠B1QA,
∴△PB1D∽△B1QA,
∴$\frac{PD}{A{B}_{1}}=\frac{P{B}_{1}}{{B}_{1}Q}=2$,
∴B1A=1,
∴OB1=3,即点B1(3,0);
(2)∵四边形OABC为平行四边形,OA=4,OC=2,且OC⊥AC,
∴∠OAC=30°,
∴点C(1,$\sqrt{3}$),
∵B1E:B1F=1:3,
∴点B1不与点E,F重合,也不在线段EF的延长线上,
①当点B1在线段FE的延长线上时,如图2,延长B1F与y轴交于点G,点B1的横坐标为m,B1F∥x轴,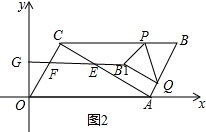
B1E:B1F=1:3,
∴B1G=m,
设OG=a,
则GF=$\frac{\sqrt{3}}{3}a$,OF=$\frac{2\sqrt{3}}{3}a$,
∴CF=$2-\frac{2\sqrt{3}}{3}a$,
∴EF=$4-\frac{4\sqrt{3}}{3}a$,B1E=$2-\frac{2\sqrt{3}}{3}a$,
∴B1G=B1E+EF+FG=$(2-\frac{2\sqrt{3}}{3}a)+(4-\frac{4\sqrt{3}}{3}a)+\frac{\sqrt{3}}{3}a=m$,
∴a=$-\frac{\sqrt{3}}{5}m+\frac{6}{5}\sqrt{3}$,即B1的纵坐标为$-\frac{\sqrt{3}}{5}m+\frac{6}{5}\sqrt{3}$,
如图2-1中,当点Q与A重合时,可得点B′横坐标的最小值,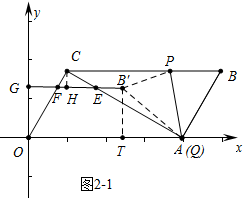
作CH⊥EF于H,B′T⊥OA于T,设FH=n,则CF=2n,EF=4n,EB′=2n,OF=2-2n,FG=1-n,GB=1+5n,
在Rt△AB′T中,易知TB′=OG=$\sqrt{3}$(1-n),AB′=2,AT=4-(1+5n)=3-5n,
∴[$\sqrt{3}$(1-n)]2+(3-5n)2=22,
解得n=$\frac{2}{7}$或-1(舍弃),
∴GB′=1+$\frac{10}{7}$=$\frac{17}{7}$,
如图2-2中,当点P与A重合时,可得点B′横坐标的最大值,
作CH⊥EF于H,设FH=n,则CF=2n,EF=4n,EB′=2n,OF=2-2n,FG=1-n,GB=1+5n,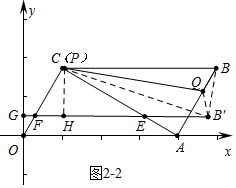
在Rt△CB′H中,易知CH=$\sqrt{3}$n,HB′=5n,CB′=CB=4,
∴($\sqrt{3}$n)2+(5n)2=42,
解得n=$\frac{2\sqrt{7}}{7}$,
∴GB′=1+5n=1+$\frac{10\sqrt{7}}{7}$,
∴m的取值范围是$\frac{17}{7}$≤m≤1+$\frac{10}{7}$$\sqrt{7}$;
②当点B1在线段EF(除点E,F)上时,如图3,延长B1F与y轴交于点G,点B1的横坐标为m,B1F∥x轴,
B1E:B1F=1:3,
∴B1G=m,
设OG=a,
则GF=$\frac{\sqrt{3}}{3}a$,OF=$\frac{2\sqrt{3}}{3}a$,
∴CF=$2-\frac{2\sqrt{3}}{3}a$,
∴FE=$4-\frac{4\sqrt{3}}{3}a$,B1F=$\frac{3}{4}EF=3-\sqrt{3}a$,
∴B1G=B1F+FG=$(3-\sqrt{3}a)+\frac{\sqrt{3}}{3}a=m$,
∴a=$-\frac{\sqrt{3}}{2}m+\frac{3}{2}\sqrt{3}$,即点B1的纵坐标为$-\frac{\sqrt{3}}{2}m+\frac{3}{2}\sqrt{3}$,
同法可得m的取值范围是$\frac{15}{7}≤m≤3$.
点评 此题考查四边形的综合题,关键是利用平行四边形的性质,分点在线段EF的延长线和线段上两种情况进行分析.


科目:初中数学 来源: 题型:选择题
| A. | 2.905×108 | B. | 2.905×109 | C. | 2.905×1010 | D. | 2.905×1011 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
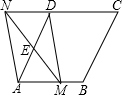 如图,在菱形ABCD中,AB=2,∠BAD=60°,E是边AD的中点,M是边AB上任一点(不与点A重合),延长ME交CD的延长线与点N,连接MD,AN.
如图,在菱形ABCD中,AB=2,∠BAD=60°,E是边AD的中点,M是边AB上任一点(不与点A重合),延长ME交CD的延长线与点N,连接MD,AN.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\root{3}{0.177}$≈0.5615 | B. | $\root{3}{0.0177}$≈0.5615 | C. | $\root{3}{1.77}$≈0.5165 | D. | $\root{3}{17.7}$≈56.15 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在△ABC中,∠C=90°,AB=30,D是AB上一点,AD:CD=25:7,且DB=DA,过AB上一点P,作PE⊥AC于E,PF⊥BD于F,则PE+PF长是18.
如图,在△ABC中,∠C=90°,AB=30,D是AB上一点,AD:CD=25:7,且DB=DA,过AB上一点P,作PE⊥AC于E,PF⊥BD于F,则PE+PF长是18.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
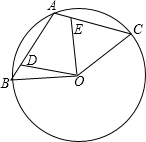 已知A、B、C是圆O上的三个点,其中点A是弧BC的中点,连接AB、AC,点D、E分别在弦AB、AC上,且满足AD=CE.
已知A、B、C是圆O上的三个点,其中点A是弧BC的中点,连接AB、AC,点D、E分别在弦AB、AC上,且满足AD=CE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 8 | B. | 4 | C. | 2 | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com