练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    8．如图，已知四边形ABEC内接于⊙O，点D在AC的延长线上，CE平分∠BCD交⊙O于点E，则下列结论中一定正确的是（　　）
    A．AB=AEB．AB=BEC．AE=BED．AB=AC

    分析 只要证明∠ECB=∠BAE，∠ECD=∠ABE，再根据角平分线定义即可解决问题．

    解答 解：连接EC．
    ∵EC平分∠BCD，
    ∴∠ECB=∠ECD，
    ∵∠ECB=∠BAE，∠ECD=∠ABE，
    ∴∠BAE=∠ABE，
    ∴EA=EB．
    故选C．

    点评 本题考查圆的有关性质、圆内接四边形的性质等知识，解题的关键是灵活运用这些知识解决问题，属于基础题，中考常考题型．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    4．如图，正方形ABCD的边长为1，AC，BD是对角线．将△DCB绕着点D顺时针旋转45°得到△DGH，HG交AB于点E，连接DE交AC于点F，连接FG．则下列结论：
    ①四边形AEGF是菱形
    ②△AED≌△GED
    ③∠DFG=112.5°
    ④BC+FG=1.5
    其中正确的结论是①②③．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    5．如图，四边形ABCD的对角线AC、BD相交于点O，△ABO≌△ADO．下列结论：
    ①AC⊥BD；②CB=CD；③△ABC≌△ADC；④DA=DC．
    其中所有正确结论的序号是①②③．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．如图①，直线y=$\frac{4}{3}$x+4交于x轴于点A，交y轴于点C，过A、C两点的抛物线F1交x轴于另一点B（1，0）．
    （1）求抛物线F1所表示的二次函数的表达式；
    （2）若点M是抛物线F1位于第二象限图象上的一点，设四边形MAOC和△BOC的面积分别为S四边形MAOC和S△BOC，记S=S四边形MAOC-S△BOC，求S最大时点M的坐标及S的最大值；
    （3）如图②，将抛物线F1沿y轴翻折并“复制”得到抛物线F2，点A、B与（2）中所求的点M的对应点分别为A′、B′、M′，过点M′作M′E⊥x轴于点E，交直线A′C于点D，在x轴上是否存在点P，使得以A′、D、P为顶点的三角形与△AB′C相似？若存在，请求出点P的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．如图①，在△ABC中，AB=7，tanA=$\frac{3}{4}$，∠B=45°．点P从点A出发，沿AB方向以每秒1个单位长度的速度向终点B运动（不与点A、B重合），过点P作PQ⊥AB．交折线AC-CB于点Q，以PQ为边向右作正方形PQMN，设点P的运动时间为t（秒），正方形PQMN与△ABC重叠部分图形的面积为S（平方单位）．
    （1）直接写出正方形PQMN的边PQ的长（用含t的代数式表示）．
    （2）当点M落在边BC上时，求t的值．
    （3）求S与t之间的函数关系式．
    （4）如图②，点P运动的同时，点H从点B出发，沿B-A-B的方向做一次往返运动，在B-A上的速度为每秒2个单位长度，在A-B上的速度为每秒4个单位长度，当点H停止运动时，点P也随之停止，连结MH．设MH将正方形PQMN分成的两部分图形面积分别为S1、S2（平方单位）（0＜S1＜S2），直接写出当S2≥3S1时t的取值范围．

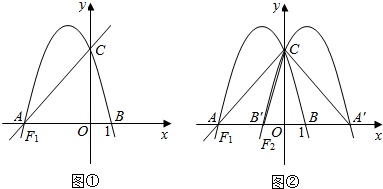
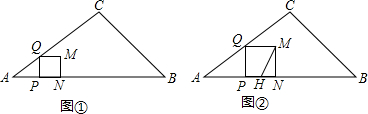
    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    13．一组数2，1，1，x，1，y，…，满足“从第三个数起，每个数都等于它前面的两个数之差”，那么这组数中y表示的数为（　　）
    A．-1B．3C．5D．-5

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    20．在大课间活动中，体育老师对甲、乙两名同学每人进行10次立定跳远测试，他们的平均成绩相同，方差分别是S${\;}_{甲}^{2}$=0.20，${S}_{乙}^{2}$=0.16，则甲、乙两名同学成绩比较稳定的是乙．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．化简：（a+3）2-a（a+2）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

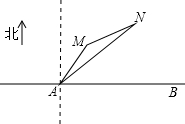    18．如图，公路AB为东西走向，在点A北偏东36.5°方向上，距离5千米处是村庄M；在点A北偏东53.5°方向上，距离10千米处是村庄N（参考数据；sin36.5°=0.6，cos36.5°=0.8，tan36.5°=0.75，sin23.6°=0.4，cos66.4°=0.4，tan21.8°=0.4）．
    （1）求M，N两村之间的距离；
    （2）试问村庄N在村庄M的什么方向上？（精确到0.1度）

    查看答案和解析>>

    同步练习册答案