
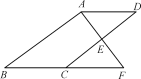
【题目】如图,E是□ABCD的边CD的中点,延长AE交BC的延长线于点F.
(1)求证:AE=EF;
(2)若∠BAF=90°,BC=15,EF=9,求CD的长.
【答案】(1)详见解析;(2)CD=24
【解析】
(1)要证明AE=EF,只要证明△AED≌△FEC即可,根据平行四边形的性质和全等三角形的判定即可解答本题;
(2)根据(1)中的结论和勾股定理、平行四边形的性质可以求得CD的长.
(1)证明:∵四边形ABCD是平行四边形,点E时CD的中点,
∴AD∥BF,ED=EC,
∴∠D=∠ECF,
在△AED和△FEC中,
∠D=∠ECF,ED=EC,∠AED=∠FEC,
∴△AED≌△FEC(ASA),
∴AE=EF;
(2)由(1)知△AED≌△FEC,
∴AD=FC,
∵四边形ABCD是平行四边形,∠BAF=90°,BC=15,EF=9,AE=![]() AF,
AF,
∴AD=BC=15,AB=CD,AF=2EF=18,
∴BF=2BC=30,
∴在Rt△ABF中,由勾股定理得:AB=![]() ,
,
∴CD=AB=24.


科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.若 a、b、c是△ABC的三边,则a2+b2=c2
B.若 a、b、c是Rt△ABC的三边,则a2+b2=c2
C.若 a、b、c是Rt△ABC的三边,![]() ,则a2+b2=c2
,则a2+b2=c2
D.若 a、b、c是Rt△ABC的三边,![]() ,则a2+b2=c2
,则a2+b2=c2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠MON=30°,点A1,A2,A3,…在射线ON上,点B1,B2,B3,…在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4,…均为等边三角形,若OA2=4,则△AnBnAn+1的边长为__________.
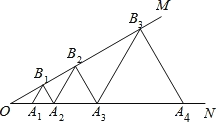
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高学生对毒品危害性的认识,我市相关部门每个月都要对学生进行“禁毒知识应知应会”测评.为了激发学生的积极性,某校对达到一定成绩的学生授予“禁毒小卫士”的荣誉称号.为了确定一个适当的奖励目标,该校随机选取了七年级20名学生在5月份测评的成绩.数据如下:
收集数据:90 91 89 96 90 98 90 97 91 98 99 97 91 88 90 97 95 90 95 88
整理、描述数据:
成绩/分 | 88 | 89 | 90 | 91 | 95 | 96 | 97 | 98 | 99 |
学生人数 | 2 | 1 |
| 3 | 2 | 1 |
| 2 | 1 |
数据样本数据的平均数、众数和中位数如下表
平均数 | 众数 | 中位数 |
93 |
|
|
应用数据
(1)由上表填空:![]() ________,
________,![]() ________,
________,![]() ________,
________,![]() ________,
________,
(2)根据所给数据,如果该校想确定七年级前![]() 的学生为“良好”等次,你认为“良好”等次的测评成绩至少定为________分.
的学生为“良好”等次,你认为“良好”等次的测评成绩至少定为________分.
(3)根据数据分析,该校决定在七年级授予测评成绩前![]() 的学生“禁毒小卫士”荣誉称号.请估计评选该荣誉称号的最低分数,并说明理由.
的学生“禁毒小卫士”荣誉称号.请估计评选该荣誉称号的最低分数,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,∠BCD=90°,∠ABC=45°,AD=CD,CE平分∠ACB交AB于点E,在BC上截取BF=AE,连接AF交CE于点G,连接DG交AC于点H,过点A作AN⊥BC,垂足为N,AN交CE于点M.则下列结论;①CM=AF;②CE⊥AF;③△ABF∽△DAH;④GD平分∠AGC,其中正确的序号是__________.
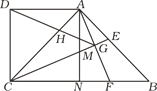
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 的图象如图所示,点
的图象如图所示,点![]() 位于坐标原点, 点
位于坐标原点, 点![]() ,
,![]() ,
,![]() ,…,
,…,![]() 在y轴的正半轴上,点
在y轴的正半轴上,点![]() ,
,![]() ,
,![]() ,…,
,…,![]() 在二次函数
在二次函数![]() 位于第一象限的图象上,若△
位于第一象限的图象上,若△![]() ,△
,△![]() ,△
,△![]() ,…,
,…,![]() 都为等边三角形,则
都为等边三角形,则![]() 的边长= .
的边长= .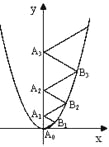
查看答案和解析>>
科目:初中数学 来源: 题型:
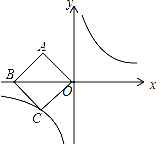
【题目】如图,在平面直角坐标系中,正方形ABCO的对角线BO在x轴上,若正方形ABCO的边长为4![]() ,点B在x负半轴上,反比例函数的图象经过C点.
,点B在x负半轴上,反比例函数的图象经过C点.
(1)求该反比例函数的解析式;
(2)若点P是反比例函数上的一点,且△PBO的面积恰好等于正方形ABCO的面积,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】赵爽弦图是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形,如图所示,若这四个全等直角三角形的两条直角边分别平行于x轴和y轴,大正方形的顶点B1、C1、C2、C3、…、Cn在直线y=﹣![]() 上,顶点D1、D2、D3、…、Dn在x轴上,则第n个阴影小正方形的面积为__.
上,顶点D1、D2、D3、…、Dn在x轴上,则第n个阴影小正方形的面积为__.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() .
.
(1)求出该函数图象的顶点坐标,对称轴,图象与![]() 轴、
轴、![]() 轴的交点坐标;
轴的交点坐标;
(2)![]() 在什么范围内时,
在什么范围内时,![]() 随
随![]() 的增大而增大?当
的增大而增大?当![]() 在什么范围内时,
在什么范围内时,![]() 随
随![]() 的增大而减小?
的增大而减小?
(3)当![]() 在什么范围内时,
在什么范围内时,![]() ?
?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com