
【题目】如图,边长为2的正方形ABCD的顶点A、B在一个半径为2的圆上,顶点C、D在该圆内.将正方形ABCD绕点A逆时针旋转,当点D第一次落在圆上时,点C旋转到C′,则∠C′AB=__°.
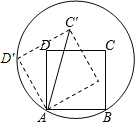
【答案】75
【解析】
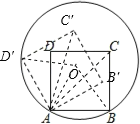
如图,分别连接OA、OB、OD′、OC、OC′,证明△OAB和△OAD′都为等边三角形,则∠OAB=∠OAD′=60°,所以∠D′AB=120°;再证明∠D′AC′=45°,然后计算∠D′AB﹣∠D′AC′即可.
解:如图,分别连接OA、OB、OD′、OC、OC′;
∵OA=OB=AB,
∴△OAB是等边三角形,
∴∠OAB=60°;
同理可得△OAD′为等边三角形,
∴∠OAD′=60°,
∴∠D′AB=60°+60°=120°;
∵AC′为正方形AB′C′D′的对角线,
∴∠D′AC′=45°,
∴∠C′AB=∠D′AB﹣∠D′AC′=120°﹣45°=75°.
故答案为:75.


 寒假学与练系列答案
寒假学与练系列答案科目:初中数学 来源: 题型:
【题目】“佳佳商场”在销售某种进货价为20元/件的商品时,以30元/件售出,每天能售出100件.调查表明:这种商品的售价每上涨1元/件,其销售量就将减少2件.
(1)为了实现每天1600元的销售利润,“佳佳商场”应将这种商品的售价定为多少?
(2)物价局规定该商品的售价不能超过40元/件,“佳佳商场”为了获得最大的利润,应将该商品售价定为多少?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是半圆O的直径,C是半圆上一个动点(不与点A,B重合),D是弦AC上一点,过点D作DE⊥AB,垂足为E,过点C作半圆O的切线,交ED的延长线于点F.
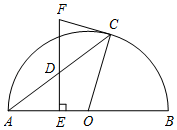
(1)求证:FC=FD.
(2)①当∠CAB的度数为 时,四边形OEFC是矩形;②若D是弦AC的中点,⊙O的半径为5,AC=8,则FC的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,在矩形ABCD中,点N为边BC上不与B、C重合的一个动点,过点N作MN⊥BC交AD于点M,交BD于点E,以MN为对称轴折叠矩形ABNM,点A、B的对应点分别是G、F,连接EF、DF,若AB=6,BC=8,当△DEF为直角三角形时,CN的长为______.
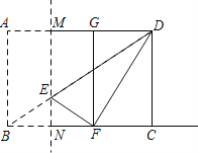
查看答案和解析>>
科目:初中数学 来源: 题型:
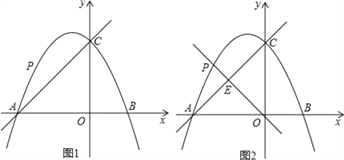
【题目】在平面直角坐标系中,抛物线y=﹣![]() x2+bx+c与x轴交于点A,B,与y轴交于点C,直线y=x+4经过A,C两点.
x2+bx+c与x轴交于点A,B,与y轴交于点C,直线y=x+4经过A,C两点.
(1)求抛物线的解析式;
(2)在AC上方的抛物线上有一动点P.
①如图1,当点P运动到某位置时,以AP,AO为邻边的平行四边形第四个顶点恰好也在抛物线上,求出此时点P的坐标;
②如图2,过点O,P的直线y=kx交AC于点E,若PE:OE=3:8,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某滑雪场举办冰雪嘉年华活动,采用直升机航拍技术拍摄活动盛况,如图,通过直升机的镜头C观测到水平雪道一端A处的俯角为30°,另一端B处的俯角为45°.若直升机镜头C处的高度CD为200米,点A、D、B在同一直线上,则雪道AB的长度为( )

A.200 米B.(200+200![]() )米
)米
C.600 米D.(200+20![]() )米
)米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 某学校为了了解八年级学生的课外阅读情况,随机抽查部分学生,并对其4月份的课外阅读量进行统计分析,绘制成如图所示的统计图(数据不完整).

根据图示信息,解答下列问题:
(1)本次被抽查的学生共有______人;
(2)a=______,b=______,将条形统计图补充完整;
(3)课外阅读量的众数是______本;
(4)若规定:4月份阅读3本以上(含3本)课外书籍者为完成阅读任务,据此估计该校八年级800名学生中,完成4月份课外阅读任务的约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
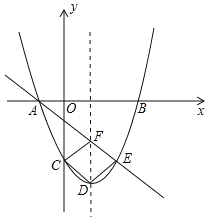
【题目】如图,二次函数y=x2+bx+c的图象与x轴相交于点A、B两点,与y轴相交于点C(0,﹣3),抛物线的对称轴为直线x=1.
(1)求此二次函数的解析式;
(2)若抛物线的顶点为D,点E在抛物线上,且与点C关于抛物线的对称轴对称,直线AE交对称轴于点F,试判断四边形CDEF的形状,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com