
【题目】如图,抛物线y=ax2+bx+c交x轴分别于点A(﹣3,0),B(1,0),交y轴正半轴于点D,抛物线顶点为C.下列结论:①2a﹣b=0;②a+b+c=0;③a﹣b>am2+bm;④当△ABC是等腰直角三角形时,a=﹣0.5;⑤若D(0,3),则抛物线的对称轴直线x=﹣1上的动点P与B、D两点围成的△PBD周长最小值为![]() .其中,正确的个数为_____.
.其中,正确的个数为_____.

【答案】4
【解析】
利用待定系数法,二次函数的性质,等腰直角三角形的性质,两点之间线段最短一一判断即可.
解:把A(﹣3,0),B(1,0)代入y=ax2+bx+c得到 ![]() ,
,
消去c得到2a﹣b=0,故①②正确,
∵抛物线的对称轴直线x=![]() =﹣1,开口向下,
=﹣1,开口向下,
∴x=﹣1时,y有最大值,最大值=a﹣b+c,
∵m≠﹣1,
∴a﹣b+c>am2+bm+c,
∴a﹣b>am2+bm,故③正确,
当△ABC是等腰直角三角形时,则CE=BE=2,
∴C(﹣1,2),
可以假设抛物线的解析式为y=a(x+1)2+2,把(1,0)代入得到a=﹣0.5,故④正确,
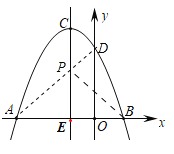
如图,连接AD交抛物线的对称轴于P,连接PB,此时△BDP的周长最小,最小值=PD+PB+BD=PD+PA+BD=AD+BD,
∵AD=![]() =3
=3![]() ,BD=
,BD=![]() =
=![]() ,
,
∴△△PBD周长最小值为3![]() +
+![]() ,故⑤错误.
,故⑤错误.
故答案为4.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
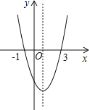
【题目】二次函数![]() 的图象如图所示,给出下列说法:
的图象如图所示,给出下列说法:
①![]() ;②方程
;②方程![]() 的根为
的根为![]() ,
,![]() ;③
;③![]() ;④当
;④当![]() 时,
时,![]() 随
随![]() 值的增大而增大;⑤当
值的增大而增大;⑤当![]() 时,
时,![]() .其中,正确的说法有________(请写出所有正确说法的序号).
.其中,正确的说法有________(请写出所有正确说法的序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
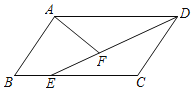
【题目】如图,在平行四边形ABCD中,E为BC边上一点,连接DE,点F为线段DE上一点,且∠AFE=∠B.
(1)求证△ADF∽△DEC;
(2)若BE=2,AD=6,且DF=![]() DE,求DF的长度.
DE,求DF的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,△ABC,△CDE都是等边三角形.
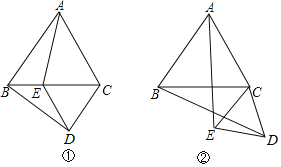
(1)写出AE与BD的大小关系.
(2)若把△CDE绕点C逆时针旋转到图②的位置时,上述(1)的结论仍成立吗?请说明理由.
(3)△ABC的边长为5,△CDE的边长为2,把△CDE绕点C逆时针旋转一周后回到图①位置,求出线段AE长的最大值和最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司研制出新产品,该产品的成本为每件2400元.在试销期间,购买不超过10件时,每件销售价为3000元;购买超过10件时,每多购买一件,所购产品的销售单价均降低5元,但最低销售单价为2600元。请解决下列问题:
(1)直接写出:购买这种产品 ________件时,销售单价恰好为2600元;
(2)设购买这种产品x件(其中x>10,且x为整数),该公司所获利润为y元,求y与x之间的函数表达式;
(3)该公司的销售人员发现:当购买产品的件数超过10件时,会出现随着数量的增多,公司所获利润反而减少这一情况.为使购买数量越多,公司所获利润越大,公司应将最低销售单价调整为多少元?(其它销售条件不变)
查看答案和解析>>
科目:初中数学 来源: 题型:
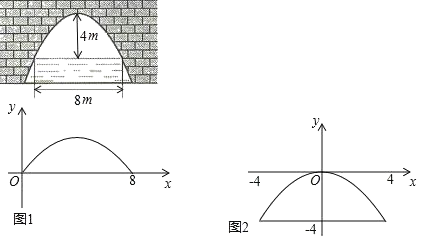
【题目】图中所示的抛物线形拱桥,当拱顶离水面4m时,水面宽8m.水面上升3米,水面宽度减少多少?下面给出了解决这个问题的两种建系方法.
方法一如图1,以上升前的水面所在直线与抛物线左侧交点为原点,以上升前的水面所在直线为x轴,建立平面直角坐标系xOy;
方法二如图2,以抛物线顶点为原点,以抛物线的对称轴为y轴,建立平面直角坐标系xOy,
查看答案和解析>>
科目:初中数学 来源: 题型:
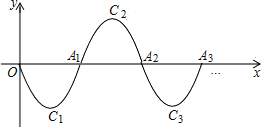
【题目】如图一段抛物线y=x2﹣3x(0≤x≤3),记为C1,它与x轴于点O和A1:将C1绕旋转180°得到C2,交x轴于A2;将C2绕旋转180°得到C3,交x轴于A3,如此进行下去,若点P(2020,m)在某段抛物线上,则m的值为( )
A.0B.﹣![]() C.2D.﹣2
C.2D.﹣2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解同学们每月零花钱的数额,校园小记者随机调查了本校部分同学,根据调查结果,绘制出了如下两个尚不完整的统计图表.
调查结果统计表
组别 | 分组(单位:元) | 人数 |
A | 0≤x<30 | 4 |
B | 30≤x<60 | 16 |
C | 60≤x<90 | a |
D | 90≤x<120 | b |
E | x≥120 | 2 |
请根据以上图表,解答下列问题:
(1)填空:这次被调查的同学共有__人,a+b=__,m=___;
(2)求扇形统计图中扇形C的圆心角度数;
(3)该校共有学生1000人,请估计每月零花钱的数额x在60≤x<120范围的人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,折叠边长为![]() 的正方形
的正方形![]() ,使点
,使点![]() 落在边
落在边![]() 上的点
上的点![]() 处(不与点
处(不与点![]() ,
,![]() 重合),点
重合),点![]() 落在点
落在点![]() 处,折痕
处,折痕![]() 分别与边
分别与边![]() 、
、![]() 交于点
交于点![]() 、
、![]() ,
,![]() 与边
与边![]() 交于点
交于点![]() .证明:
.证明:
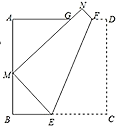
(1)![]() ;
;
(2)若![]() 为
为![]() 中点,则
中点,则![]() ;
;
(3)![]() 的周长为
的周长为![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com