
 如图,矩形ABCD中,∠FCD=75°,以CF为一边的等边△EFC的另一顶点E在AD上,点K是FC的中点
如图,矩形ABCD中,∠FCD=75°,以CF为一边的等边△EFC的另一顶点E在AD上,点K是FC的中点分析 (1)要证明矩形ABCD是正方形,只要证明邻边相等就行,可通过证明△CDE≌△CBF实现;
(2)因为△EFC是等边三角形,要证明CE2=4BC•FB,可证明EF2=CF2=CE2=4BC•FB;由(1)知BF=CD,AD=AB,∴BC=BF+AF,AF2=(BC-BF)2=BC2+BF2-2BC•BF,即AF2+2BC•BF=BC2+BF2=FC2=CE2,所以2AF2+4BC•BF=2FC2=2CE2,在Rt△AEF中,易证2AF2=EF2=CE2,变形得证.
(3)连接EK,易证∠EKC=∠ADC=90°,所以点E、K、C、D四点共圆,通过同弧上的圆周角相等,可得到∠KDC的度数.
解答 (1)证明:∵ABCD是矩形,
∴∠B=∠BCD=∠ADC=90°,
∵∠FCD=75°,∴∠FCB=15°,
∵△EFC是等边三角形,
∴CF=CE,∠ECF=60°,
∴∠ECD=∠FCD-∠FCE=15°=∠FCB.
在△CDE和△CBF中,$\left\{\begin{array}{l}{∠B=∠ADC}\\{∠ECD=∠FCB}\\{CE=CF}\end{array}\right.$,
∴△CDE≌△CBF.
∴BC=CD.
∴矩形ABCD是正方形.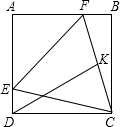
(2)证明:∵△EFC是等边三角形,
∴CE=EF=CF,
∵△CDE≌△CBF,
∴BF=ED,
∵ABCD是正方形,
∴AB=AD=BC,
∴AE=AF.
∵BC=BF+AF,AF2=(BC-BF)2=BC2+BF2-2BC•BF,即AF2+2BC•BF=BC2+BF2=FC2=CE2,
∴2AF2+4BC•BF=2FC2=2CE2.
在Rt△AEF中,EF2=AE2+AF2=2AF2=CE2,
∴CE2+4BC•BF=2CE2,即CE2=4BC•BF.
(3)解:连接EK.
∵△EFC是等边三角形,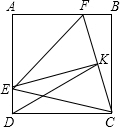
点K是FC的中点,
∴EK⊥CF,∠KEC=30°,
∴∠EKC=∠ADC=90°,
∴E、K、C、D四点共圆,
∴∠KDC=∠KEC=30°.
点评 本题考查了正方形的判定和性质、等边三角形的性质、三角形全等的判定、勾股定理、四点共圆及圆周角定理.第二问的恒等变形,是通过完全平方公式和边的和差变化实现的,第三问易可通过证明△EBC∽△FBK求解.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 10n | B. | $\frac{n}{10}$ | C. | 10m | D. | $\frac{m}{10}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
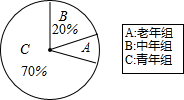 2015年12月,某市总工会组织该市各单位参加“迎新春长跑活动”,组委会将男运动员分成三组:老年组、中年组和青年组,根据报名情况,制作了如图所示的人数扇形统计图,已知青年组共有210人,则老年组共有30人.
2015年12月,某市总工会组织该市各单位参加“迎新春长跑活动”,组委会将男运动员分成三组:老年组、中年组和青年组,根据报名情况,制作了如图所示的人数扇形统计图,已知青年组共有210人,则老年组共有30人.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,∠C=90°,BC、AC、AB边的长分别记为a、b、c,点E是BC边上一个动点(点E与点B、C不重合),连接AE.已知a、b满足$\left\{\begin{array}{l}{b-6=0}\\{2a-b=10}\end{array}\right.$,且c是不等式组$\left\{\begin{array}{l}{\frac{x+12}{4}≤x+6}\\{\frac{2x+2}{3}>x-3}\end{array}\right.$的最大整数解.
如图,在△ABC中,∠C=90°,BC、AC、AB边的长分别记为a、b、c,点E是BC边上一个动点(点E与点B、C不重合),连接AE.已知a、b满足$\left\{\begin{array}{l}{b-6=0}\\{2a-b=10}\end{array}\right.$,且c是不等式组$\left\{\begin{array}{l}{\frac{x+12}{4}≤x+6}\\{\frac{2x+2}{3}>x-3}\end{array}\right.$的最大整数解.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 进价(元/只) | 售价(元/只) | |
| 甲种节能灯 | 30 | 40 |
| 乙种节能灯 | 35 | 50 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 阅读下面材料:在数学课上,老师提出如下问题:
阅读下面材料:在数学课上,老师提出如下问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com