
分析 根据三角形的外心定义对①进行判断;利用分类讨论的思想对②③进行判断;根据不等式的性质对④进行判断.
解答 解:三角形的外心是三角形三边垂直平分线的交点,所以①正确;
函数y=(1-a)x2-4x+6与x轴只有一个交点,则a=$\frac{1}{3}$或1,所以②错误;
半径分别为1和2的两圆相切,则两圆的圆心距为1或3;
若对于任意x>1的实数,都有ax>1成立,则a的取值范围是a≥1,所以④正确.
故答案为:①④.
点评 本题考查了命题与定理:判断一件事情的语句,叫做命题.许多命题都是由题设和结论两部分组成,题设是已知事项,结论是由已知事项推出的事项,一个命题可以写成“如果…那么…”形式.有些命题的正确性是用推理证实的,这样的真命题叫做定理.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
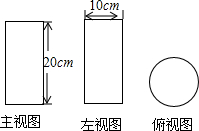 某商品的外包装盒的三视图如图所示,则这个包装盒的体积是( )
某商品的外包装盒的三视图如图所示,则这个包装盒的体积是( )| A. | 200πcm3 | B. | 500πcm3 | C. | 1000πcm3 | D. | 2000πcm3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知BC是⊙O的弦,A是⊙O外一点,△ABC为正三角形,D为BC的中点,M为⊙O上一点,并且∠BMC=60°.
如图,已知BC是⊙O的弦,A是⊙O外一点,△ABC为正三角形,D为BC的中点,M为⊙O上一点,并且∠BMC=60°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
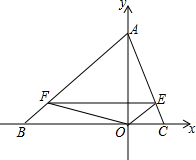 如图,等腰△ABC中,BA=BC,AO=3CO=6.动点F在BA上以每分钟5个单位长度的速度从B点出发向A点移动,过F作FE∥BC交AC边于E点,连结FO、EO.
如图,等腰△ABC中,BA=BC,AO=3CO=6.动点F在BA上以每分钟5个单位长度的速度从B点出发向A点移动,过F作FE∥BC交AC边于E点,连结FO、EO.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com