
| |||||||||||||||
(1) |
从图乙知甲鱼池的个数为26个,从图甲知甲鱼池的产量为1.2万只.所以第2年全县甲鱼总产量为26x 1.2=31.2万只 |
(2) |
由题设条件知:第1年全县的甲鱼养殖总数=30×1=30万只;第6年全县的甲鱼养殖总数=10×2=20万只;所以第6年比第1年全县的甲鱼养殖规模是缩小了 |
(3) |
图甲是经过两点(2,1.2)(6,2)的线段,其解析式为y1=0.2x+0.8(1≤x≤6,x为正整数),图乙是经过两点(1,30),(6,10)的线段,其解析式为y2=-4x+34(1≤x≤6,x是正整数). 设全县每年甲鱼养殖总数为y万只,则有y=y1·y2=(0.2x+0.8)(-4x+34)(x是正整数),即y=-0.8(x-2.25)2+31.25,所以当x=2.25≈2年时,全县甲鱼养殖规模最大 |


 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
 只鳗鱼上升到第6年2万只.乙调查表明:全县鱼池总个数由第1年30个减少到第6年10个.
只鳗鱼上升到第6年2万只.乙调查表明:全县鱼池总个数由第1年30个减少到第6年10个.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
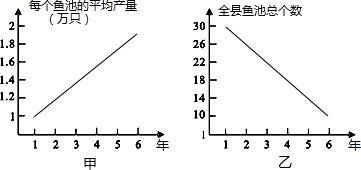 只鳗鱼上升到第6年2万只.乙调查表明:全县鱼池总个数由第1年30个减少到第6年10个.
只鳗鱼上升到第6年2万只.乙调查表明:全县鱼池总个数由第1年30个减少到第6年10个.查看答案和解析>>
科目:初中数学 来源:2010年湖北省武汉市华师一附中自主招生考试数学试卷 (解析版) 题型:解答题
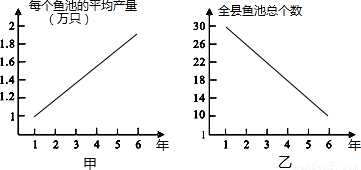
查看答案和解析>>
科目:初中数学 来源:2012年北师大版初中数学八年级上6.5一次函数图象的应用练习卷(解析版) 题型:解答题
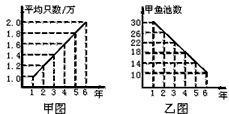
甲乙两人连续6年对某县农村甲鱼养殖业的规模(产量)进行调查,提供了两个方面的信息,如甲乙两图.甲调查表明:每个甲鱼池平均生产量从第一年1万只甲鱼上升到第6年的2万只;乙调查表明:甲鱼池由第一年30个减少到第6年的10个.请你根据提供的信息说明

(1)第2年甲鱼池的个数及全县出产甲鱼总数;
(2)到第6年这个县的甲鱼养殖业的规模比第一年是扩大了还是缩小了?说明理由.
(3)哪一年的规模最大?说明理由.
查看答案和解析>>
科目:初中数学 来源:模拟题 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com