
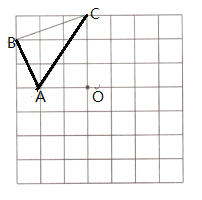
【题目】在正方形网格图中,若每个小正方形的边长是1,![]() 与
与![]() 关于点
关于点![]() 对称.
对称.
(1)画出![]() .
.
(2)![]() 与
与![]() 的位置关系是 .
的位置关系是 .
(3)点![]() 在直线
在直线![]() 上,
上,![]() 的最小值是 .
的最小值是 .
【答案】(1)见解析;(2)A1B1∥AB;(3)![]()
【解析】
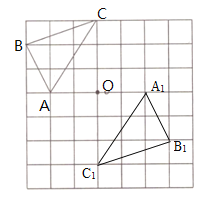
(1)分别描出A、B、C关于点O的对称点,连接即可得到![]() ;
;
(2)连接A A1,B B1,由对称性判定△AOB≌△A1OB1,得出∠ABO=∠A1B1O,即可判定A1B1∥AB;
(3)连接BA1,交OC于点P,当B、P、A1三点在一条直线上时,![]() 取得最小值,利用勾股定理即可得解.
取得最小值,利用勾股定理即可得解.
(1)如图所示:
(2)连接A A1,B B1,如图所示:

由对称性,得OA=OA1,OB=OB1,
∵∠AOB=∠A1OB1
∴△AOB≌△A1OB1(SAS)
∴∠ABO=∠A1B1O
∴A1B1∥AB;
(3)连接BA1,交OC于点P,如图所示:
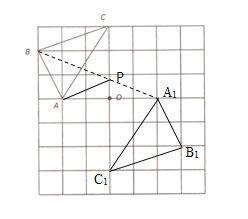
当B、P、A1三点在一条直线上时,![]() 取得最小值
取得最小值
∴![]()


科目:初中数学 来源: 题型:
【题目】春节将至,一电商平台![]() 对本年度最受消费者喜爱的某品牌辣椒酱进行促销,促销方式为:每人每次凡购买不超过15瓶的,每瓶4元,外加运费
对本年度最受消费者喜爱的某品牌辣椒酱进行促销,促销方式为:每人每次凡购买不超过15瓶的,每瓶4元,外加运费![]() 元;超过15瓶的,超过的部分每瓶减少
元;超过15瓶的,超过的部分每瓶减少![]() 元,并付运费
元,并付运费![]() 元,若设购买的瓶数为
元,若设购买的瓶数为![]() 瓶.
瓶.
(1)当![]() 时,请用含
时,请用含![]() 和
和![]() 的代数式表示购买所需费用:_______________;当
的代数式表示购买所需费用:_______________;当![]() 时,请用含
时,请用含![]() 和
和![]() 的代数式表示购买所需费用:_______________.
的代数式表示购买所需费用:_______________.
(2)王老师和李老师看到促销信息后拟打算在该平台分别购买20瓶和26瓶该品牌辣椒酱
①经过预算,两位老师在该平台购买分别花费82元和100元,请通过计算求出![]() 的值.
的值.
②你能帮两位老师设计一种更省钱的购买方案吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八年级数学学习合作小组在学过《图形的相似》这一章后,发现可将相似三角形的定义、判定以及性质拓展到矩形、菱形的相似中去.如:我们可以定义:“长和宽之比相等的矩形是相似矩形.”相似矩形也有以下的性质:相似矩形的对角线之比等于相似比,周长比等于相似比,面积比等于相似比的平方等等.请你参与这个学习小组,一同探索这类问题:
![]() 写出判定菱形相似的一种判定方法:若有一组角对应相等(或两组对角线对应成比例),则这两个菱形相似;
写出判定菱形相似的一种判定方法:若有一组角对应相等(或两组对角线对应成比例),则这两个菱形相似;
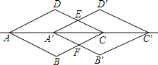
![]() 如图,将菱形
如图,将菱形![]() 沿着直线
沿着直线![]() 向右平移后得到菱形
向右平移后得到菱形![]() ,试证明:四边形
,试证明:四边形![]() 是菱形,且菱形
是菱形,且菱形![]() 菱形
菱形![]() ;
;
![]() 若
若![]() ,菱形
,菱形![]() 的面积是菱形
的面积是菱形![]() 面积的一半,求平移的距离
面积的一半,求平移的距离![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
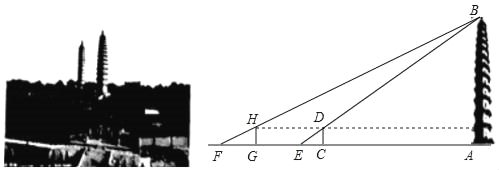
【题目】太原双塔寺又名永祚寺,是国家级文物保护单位,由于双塔(舍利塔、文峰塔)耸立,被人们称为“文笔双塔”,是太原的标志性建筑之一,某校社会实践小组为了测量舍利塔的高度,在地面上的C处垂直于地面竖立了高度为2米的标杆CD,这时地面上的点E,标杆的顶端点D,舍利塔的塔尖点B正好在同一直线上,测得EC=4米,将标杆CD向后平移到点C处,这时地面上的点F,标杆的顶端点H,舍利塔的塔尖点B正好在同一直线上(点F,点G,点E,点C与塔底处的点A在同一直线上),这时测得FG=6米,GC=53米.
请你根据以上数据,计算舍利塔的高度AB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一海轮位于灯塔P的西南方向,距离灯塔40了2海里的A处,它沿正东方向航行一段时间后,到达位于灯塔P的南偏东60°方向上的B处,求航程AB的值(结果保留根号).

查看答案和解析>>
科目:初中数学 来源: 题型:
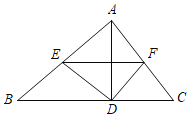
【题目】如图,在△ABC中,AD是高,E、F分别是AB、AC的中点.
(1)AB=12,AC=9,求四边形AEDF的周长;
(2)EF与AD有怎样的位置关系?证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com