
分析 (1)根据方程的系数结合根的判别式,即可得出△=20-4m≥0,解之即可得出结论;
(2)由根与系数的关系可得x1+x2=6①、x1•x2=m+4②,分x2≥0和x2<0可找出3x1=x2+2③或3x1=-x2+2④,联立①③或①④求出x1、x2的值,进而可求出m的值.
解答 解:(1)∵关于x的一元二次方程x2-6x+m+4=0有两个实数根x1,x2,
∴△=(-6)2-4(m+4)=20-4m≥0,
解得:m≤5,
∴m的取值范围为m≤5.
(2)∵关于x的一元二次方程x2-6x+m+4=0有两个实数根x1,x2,
∴x1+x2=6①,x1•x2=m+4②.
∵3x1=|x2|+2,
当x2≥0时,有3x1=x2+2③,
联立①③解得:x1=2,x2=4,
∴8=m+4,m=4;
当x2<0时,有3x1=-x2+2④,
联立①④解得:x1=-2,x2=8(不合题意,舍去).
∴符合条件的m的值为4.
点评 本题考查了根与系数的关系以及根的判别式,解题的关键是:(1)根据方程的系数结合根的判别式,找出△=20-4m≥0;(2)分x2≥0和x2<0两种情况求出x1、x2的值.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -x2+2x | B. | -x2+6x | C. | -$\frac{x}{x+2}$ | D. | $\frac{x}{x-2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | b3•b3=2b3 | B. | (a+2)(a-2)=a2-4 | ||
| C. | (ab2)3=ab6 | D. | (8a-7b)-(4a-5b)=4a-12b |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
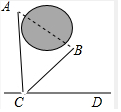 如图,A、B两个村庄之间有一个池塘,A村到公路CD的距离AC=700米,若BC═600米,∠BCD=30°,试求A、B两个村庄之间的距离(结果保留根号).
如图,A、B两个村庄之间有一个池塘,A村到公路CD的距离AC=700米,若BC═600米,∠BCD=30°,试求A、B两个村庄之间的距离(结果保留根号).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com