
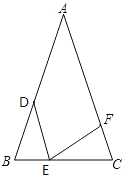
【题目】如图D、E、F分别在△ABC的三边上,BD=![]() AB,BE:EC=1:2,AC的长度是FC的3倍,四边形ADEF的面积是24,则△EFC的面积是_________.
AB,BE:EC=1:2,AC的长度是FC的3倍,四边形ADEF的面积是24,则△EFC的面积是_________.
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,双曲线y=![]() 与直线y=kx﹣2交于点A(3,1).
与直线y=kx﹣2交于点A(3,1).
(1)求直线和双曲线的解析式;
(2)直线y=kx﹣2与x轴交于点B,点P是双曲线y=![]() 上一点,过点P作直线PC∥x轴,交y轴于点C,交直线y=kx﹣2于点D.若DC=2OB,写出点P的坐标.
上一点,过点P作直线PC∥x轴,交y轴于点C,交直线y=kx﹣2于点D.若DC=2OB,写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,O为坐标原点.直线y=kx+b与抛物线y=mx2﹣![]() x+n同时经过A(0,3)、B(4,0).
x+n同时经过A(0,3)、B(4,0).
(1)求m,n的值.
(2)点M是二次函数图象上一点,(点M在AB下方),过M作MN⊥x轴,与AB交于点N,与x轴交于点Q.求MN的最大值.
(3)在(2)的条件下,是否存在点N,使△AOB和△NOQ相似?若存在,求出N点坐标,不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为深化义务教育课程改革,某校积极开展拓展性课程建设,计划开设艺术、体育、劳技、文学等多个类别的拓展性课程,要求每一位学生都自主选择一个类别的拓展性课程.为了了解学生选择拓展性课程的情况,随机抽取了部分学生进行调查,并将调查结果绘制成如下统计图(部分信息未给出):

根据统计图中的信息,解答下列问题:
(![]() )求本次被调查的学生人数.
)求本次被调查的学生人数.
(![]() )将条形统计图补充完整.
)将条形统计图补充完整.
(![]() )若该校共有
)若该校共有![]() 名学生,请估计全校选择体育类的学生人数.
名学生,请估计全校选择体育类的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点C的坐标为(4,0),一次函数![]() 的图像分别交x轴、y轴于点A、点B.
的图像分别交x轴、y轴于点A、点B.
⑴ 若点D是直线AB在第一象限内的点,且BD=BC,试求出点D的坐标.
⑵ 在⑴的条件下,若点Q是坐标轴上的一个动点,试探索在第一象限是否存在另一个点P,使得以B、D、P、Q为顶点的四边形是菱形(BD为菱形的一边)?若存在,请直接写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只不透明的口袋中原来装有1个白球、2个红球,每个球除颜色外完全相同.则下列将袋中球增减的办法中,使得将球摇匀,从中任意摸出一个球,摸到白球与摸到红球的概率不相等为( )
A. 在袋中放入1个白球 B. 在袋中放入1个白球、2个红球
C. 在袋中取出1个红球 D. 在袋中放入2个白球、1个红球
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AD=4,M是AD的中点,点E是线段AB上一动点,连接EM并延长交线段CD的延长线于点F.

(1)如图1,求证:AE=DF;
(2)如图2,若AB=2,过点M作 MG⊥EF交线段BC于点G,判断△GEF的形状,并说明理由;
(3)如图3,若AB= ![]() ,过点M作 MG⊥EF交线段BC的延长线于点G.
,过点M作 MG⊥EF交线段BC的延长线于点G.
①直接写出线段AE长度的取值范围;
②判断△GEF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O是正△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:①△BO′A可以由△BOC绕点B逆时针旋转60°得到;②点O与O′的距离为4;③∠AOB=150°;④S四边形AOBO′=6+3![]() ;⑤S△AOC+S△AOB=6+
;⑤S△AOC+S△AOB=6+![]() .其中正确的结论是
.其中正确的结论是

A. ①②③⑤ B. ①③④ C. ②③④⑤ D. ①②⑤
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com