
如图,∠AOB=90°,C、D是![]() 的三等分点,AB分别交OC,OD于点E,F,求证AE=BF=CD.
的三等分点,AB分别交OC,OD于点E,F,求证AE=BF=CD.

|
证明:连接AC,BD,因为C、D分别为 ∴ ∴AC=CD=DB,∠AOC=∠COD=∠DOB. 又∠AOB=90°, ∴∠AOC=∠COD=∠DOB=30°. 又∵OA=OC=OB, ∴△OAC为等腰三角形,△AOB为等腰直角三角形. ∴∠OAC=∠OCA=75°,∠OAB=45°, ∴∠CAE=75°-45°=30°. 在△CAE中, ∠AEC=180°-∠CAE-∠ACE=180°-30°-75°=75°. ∴∠AEC=∠ACE. ∴AC=AE. 同理可得BD=BF. ∴AE=BF=CD. |
|
圆心角定理的相关结论,只要满足其中一组量相等,那么所对的其余各组量也分别相等,是证明线段相等、弧相等、角相等的重要依据. |


科目:初中数学 来源:同步轻松练习(七年级数学下) 题型:044
如图,∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC,求∠MON的度数.

(1)若∠AOB=![]() ,其他条件不变,求∠MON的度数.
,其他条件不变,求∠MON的度数.
(2)若∠BOC=![]() (
(![]() 为锐角),其他条件不变,求∠MON的度数.
为锐角),其他条件不变,求∠MON的度数.
(3)从上面结果中能看出什么规律?
(4)线段的计算与角的计算存在着紧密联系,它们之间可以互相借鉴解法,请你模仿上述题设计一道以线段为背景的计算题,并写出其中的规律.
查看答案和解析>>
科目:初中数学 来源:边城中学2006-2007年第一学期中学数学试题 题型:022
如图,∠AOB=90°,将三角尺的直角顶点P,置于∠AOB的平分线OC上,让三角尺绕点P旋转,设三角尺的两直角边与∠AOB的两边分别交于E、F,请写出一个利用上述所有条件推出的一个正确结论(不再标注其它字母)________.
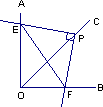
查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京市通州九年级上学期期末考试数学试卷(解析版) 题型:填空题
如图,∠AOB=90º,将Rt△OAB绕点O按逆时针方向旋转至Rt△OA′B′,使点B恰好落在边A′B′上.已知tanA= ,OB=5,则BB′=
.
,OB=5,则BB′=
.
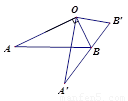
查看答案和解析>>
科目:初中数学 来源:2011年广东省汕头市潮南区中考模拟考试数学卷 题型:选择题
如图,∠AOB=90°,∠B=30°,△A′O B′可以看作是由△AOB绕点O顺时针旋转 角度得到的,若点A’在AB上,,则旋转角
角度得到的,若点A’在AB上,,则旋转角 的大小是( ).
的大小是( ).

A.90° B. 60° C.45° D.30°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com