
【题目】通过对某校营养午餐的检测,得到如下信息:每份营养午餐的总质量![]() ;午餐的成分
;午餐的成分
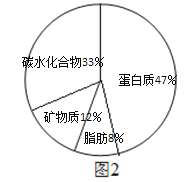
为蛋白质、碳水化合物、脂肪和矿物质,其组成成分所占比例如图![]() 所示;其中矿物质的含量是脂
所示;其中矿物质的含量是脂
肪含量的![]() 倍,蛋白质和碳水化合物含量占
倍,蛋白质和碳水化合物含量占![]() .
.

(![]() )设其中蛋白质含量是
)设其中蛋白质含量是![]() .脂肪含量是
.脂肪含量是![]() ,请用含
,请用含![]() 或
或![]() 的代数式分别表示碳水化合物和矿物
的代数式分别表示碳水化合物和矿物
质的质量.
(![]() )求每份营养午餐中蛋白质、碳水化合物、脂肪和矿物质的质量.
)求每份营养午餐中蛋白质、碳水化合物、脂肪和矿物质的质量.
(![]() )参考图
)参考图![]() ,请在图
,请在图![]() 中完成这四种不同成分所占百分比的扇形统计图.
中完成这四种不同成分所占百分比的扇形统计图.
【答案】(1)矿物质的质量为![]() ,碳水化合物的质量为
,碳水化合物的质量为![]() ;(2)蛋白质质量为
;(2)蛋白质质量为![]() ,碳水化合物质量为
,碳水化合物质量为![]() ,脂肪质量为
,脂肪质量为![]() ,矿物质质量为
,矿物质质量为![]() ;(3)见解析.
;(3)见解析.
【解析】(1)由矿物质的含量是脂肪含量的![]() 倍,即可表示出矿物质的质量,再用总质量的
倍,即可表示出矿物质的质量,再用总质量的![]() 减去矿物质的质量,即可表示出碳水化合物的质量;
减去矿物质的质量,即可表示出碳水化合物的质量;
(2)根据蛋白质和脂肪含量占![]() ,蛋白质和碳水化合物含量占
,蛋白质和碳水化合物含量占![]() ,得到关于x,y的二元一次方程组,解之即可;
,得到关于x,y的二元一次方程组,解之即可;
(3)借助关系式“某一部分的百分比=![]() ×100%×360°易得出各物质所对圆心角的度数,即可得出扇形统计图.
×100%×360°易得出各物质所对圆心角的度数,即可得出扇形统计图.
(![]() )由题可知,矿物质的质量为
)由题可知,矿物质的质量为![]() .
.
碳水化合物的质量为![]() .
.
(![]() )由题意得:
)由题意得:![]() ,
,
解得![]()
蛋白质质量为![]() .
.
碳水化合物质量为![]() ,
,
脂肪质量为![]() ,矿物质质量为
,矿物质质量为![]()
(![]() )各物质含量对应的圆心角为:
)各物质含量对应的圆心角为:
蛋白质:![]() ×360°=169.2°,
×360°=169.2°,
碳水化合物:(![]() ×360°=118.8°,
×360°=118.8°,
脂肪:(![]() ×360°=28.8°,
×360°=28.8°,
矿物质:(![]() ×360°=43.2°.
×360°=43.2°.
扇形统计图如下:


科目:初中数学 来源: 题型:
【题目】如图,矩形 ABCD 的对角线 AC 与 BD 相交于点 O,CE∥BD, DE∥AC , AD=2![]() , DE=2,则四边形 OCED 的面积为( )
, DE=2,则四边形 OCED 的面积为( )

A. 2![]() B. 4 C. 4
B. 4 C. 4![]() D. 8
D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市对进货价为10元/千克的某种苹果的销售情况进行统计,发现每天销售量y(千克)与销售价x(元/千克)存在一次函数关系,如图所示. 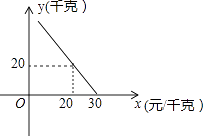
(1)求y关于x的函数关系式(不要求写出x的取值范围);
(2)应怎样确定销售价,使该品种苹果的每天销售利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2013年5月23日起,我市将对行人闯红灯分三档进行处罚,九年级数学研究学习小组在某十字路口随机调查部分市民对该法归的了解情况,统计结果后绘制了如图的三副不完整的统计图,请结合图中相关数据回答下列问题.
得分 | |
A | 50<n≤60 |
B | 60<n≤70 |
C | 70<n≤80 |
D | 80<n≤90 |
E | 90<n≤100 |
(1)本次共调查的人数为;
(2)补全频数分布图; 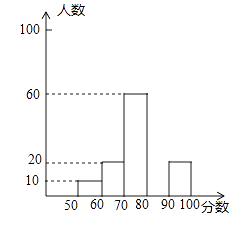
(3)在扇形统计图中,“B”所在的扇形的圆心角的度数为; 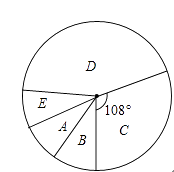
(4)若在这一周里,该路口共有2000人通过,则可估计得分在80以上的人数大约为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,CA=CB,∠ACB=90°,AB=2,点D为AB的中点,以点D为圆心作圆心角为90°的扇形DEF,点C恰在弧EF上,则图中阴影部分的面积为( )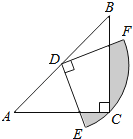
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,AC是对角线,今有较大的直角三角板,一边始终经过点B,直角顶点P在射线AC上移动,另一边交DC于点Q.
(1)如图①,当点Q在DC边上时,猜想并写出PB与PQ所满足的数量关系,并加以证明;
(2)如图②,当点Q落在DC的延长线上时,猜想并写出PB与PQ满足的数量关系,并证明你的猜想.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在东营市中小学标准化建设工程中,某学校计划购进一批电脑和电子白板,经过市场考察得知,购买1台电脑和2台电子白板需要3.5万元,购买2台电脑和1台电子白板需要2.5万元.
(1)求每台电脑、每台电子白板各多少万元?
(2)根据学校实际,需购进电脑和电子白板共30台,总费用不超过30万元,但不低于28万元,请你通过计算求出有几种购买方案,哪种方案费用最低.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将长度为8厘米的木棍截成三段,每段长度均为整数厘米.如果截成的三段木棍长度分别相同算作同一种截法(如:5,2,1和1,5,2),那么截成的三段木棍能构成三角形的概率是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com