
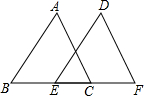
 如图,E、B、F、C四点在同一条直线上,EB=CF,∠DEF=∠ABC,添加以下哪一个条件不能判断△ABC≌△DEF的是( )
如图,E、B、F、C四点在同一条直线上,EB=CF,∠DEF=∠ABC,添加以下哪一个条件不能判断△ABC≌△DEF的是( )| A. | ∠A=∠D | B. | DF∥AC | C. | AC=DF | D. | AB=DE |
分析 由EB=CF可得出BC=EF,A、由∠A=∠D、∠ABC=∠DEF、BC=EF,利用全等三角形的判定定理AAS即可证出△ABC≌△DEF;B、由DF∥AC可得出∠ACB=∠DFE,结合BC=EF、∠ABC=∠DEF,利用全等三角形的判定定理ASA即可证出△ABC≌△DEF;C、由AC=DF结合∠ABC=∠DEF、BC=EF,无法证出△ABC≌△DEF;D、由AB=DE结合∠ABC=∠DEF、BC=EF,利用全等三角形的判定定理SAS即可证出△ABC≌△DEF.综上即可得出结论.
解答 解:∵EB=CF,
∴BC=EF.
A、在△ABC和△DEF中,$\left\{\begin{array}{l}{∠A=∠D}\\{∠ABC=∠DEF}\\{BC=EF}\end{array}\right.$,
∴△ABC≌△DEF(AAS);
B、∵DF∥AC,
∴∠ACB=∠DFE.
在△ABC和△DEF中,$\left\{\begin{array}{l}{∠ABC=∠DEF}\\{BC=EF}\\{∠ACB=∠DFE}\end{array}\right.$,
∴△ABC≌△DEF(ASA);
C、在△ABC和△DEF中,$\left\{\begin{array}{l}{∠ABC=∠DEF}\\{AC=DF}\\{BC=EF}\end{array}\right.$,
无法证出△ABC≌△DEF;
D、在△ABC和△DEF中,$\left\{\begin{array}{l}{AB=DE}\\{∠ABC=∠DEF}\\{BC=EF}\end{array}\right.$,
∴△ABC≌△DEF(SAS).
故选C.
点评 本题考查了全等三角形的判定定理,熟练掌握全等三角形的五种判定定理是解题的关键.


 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:填空题
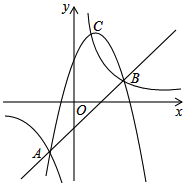 已知Y1,Y2,Y3分别表示二次函数、反比例函数和一次函数的三个函数值,它们的交点分别是A(-1,-2)、B(2,1)和C($\frac{2}{3}$,3),规定M={Y1,Y2,Y3}中最小的函数值,则下列结论:①当x<-1时,M=Y1;②当-1<x<0时,Y2<Y3<Y1;③当0≤x≤2时,M的最大值是1,无最小值;④当x≥2时,M最大值是1,无最小值.其中正确结论的个数为①②④.(填序号即可)
已知Y1,Y2,Y3分别表示二次函数、反比例函数和一次函数的三个函数值,它们的交点分别是A(-1,-2)、B(2,1)和C($\frac{2}{3}$,3),规定M={Y1,Y2,Y3}中最小的函数值,则下列结论:①当x<-1时,M=Y1;②当-1<x<0时,Y2<Y3<Y1;③当0≤x≤2时,M的最大值是1,无最小值;④当x≥2时,M最大值是1,无最小值.其中正确结论的个数为①②④.(填序号即可)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
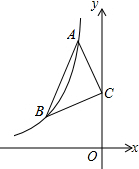 如图,△ABC的顶点A,B都在反比例函数y=-$\frac{6}{x}$的第二象限内的分支上,点C(0,3),且AC=BC,∠ACB=90°,则线段AB的长为2$\sqrt{5}$.
如图,△ABC的顶点A,B都在反比例函数y=-$\frac{6}{x}$的第二象限内的分支上,点C(0,3),且AC=BC,∠ACB=90°,则线段AB的长为2$\sqrt{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 为有效保护日益减少的水资源,某市提倡居民节约用水,并对该市居民用水采取分段收费:每户每月用水不超过20m3,每立方米收费3元;若用水超过20m3,超过部分每立方米收费5元.该市某居民家8月份交水费84元,则该居民家8月份用水量为多少m3?如果设该居民家8月份用水量为xm3,则下面所列方程中正确的是( )
为有效保护日益减少的水资源,某市提倡居民节约用水,并对该市居民用水采取分段收费:每户每月用水不超过20m3,每立方米收费3元;若用水超过20m3,超过部分每立方米收费5元.该市某居民家8月份交水费84元,则该居民家8月份用水量为多少m3?如果设该居民家8月份用水量为xm3,则下面所列方程中正确的是( )| A. | 3x+5=84 | B. | 3×20+5x=84 | C. | 3×20+5(x-20)=84 | D. | 3x+5(x-20)=84 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com