
| x | … | -3 | -2 | -1 | 0 | 1 | … |
| y | …[ | -6 | 0 | 4 | 6 | 6 | … |
| | | | | | | | |
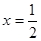 ,再根据抛物线的性质即可进行判断.根据图表,当x=-2,y=0,根据抛物线的对称形,当x=3时,y=0,即抛物线与x轴的交点为(-2,0)和(3,0);∴抛物线的对称轴是直线,
,再根据抛物线的性质即可进行判断.根据图表,当x=-2,y=0,根据抛物线的对称形,当x=3时,y=0,即抛物线与x轴的交点为(-2,0)和(3,0);∴抛物线的对称轴是直线,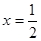 根据表中数据得到抛物线的开口向下,∴当
根据表中数据得到抛物线的开口向下,∴当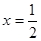 时,函数有最大值,而不是x=0,或1对应的函数值6,并且在直线
时,函数有最大值,而不是x=0,或1对应的函数值6,并且在直线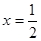 的左侧,y随x增大而增大.所以①③④正确,②错.2+bx+c的性质
的左侧,y随x增大而增大.所以①③④正确,②错.2+bx+c的性质

科目:初中数学 来源:不详 题型:解答题
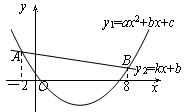
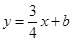 与抛物线
与抛物线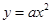 交于点A(1,
交于点A(1,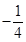 ),与
),与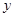 轴交于点C.
轴交于点C.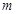 个单位(
个单位(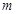 >0),抛物线与
>0),抛物线与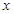 轴交于P、Q两点,过C、P、Q三点的圆恰好以CQ为直径,求
轴交于P、Q两点,过C、P、Q三点的圆恰好以CQ为直径,求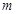 的值;
的值;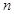 个单位(
个单位(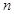 >0),抛物线与
>0),抛物线与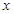 轴交于P、Q两点,过C、P、Q三点的圆的面积是否存在最小值?若存在,请求出这个最小值和此时
轴交于P、Q两点,过C、P、Q三点的圆的面积是否存在最小值?若存在,请求出这个最小值和此时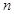 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.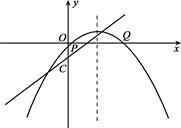
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
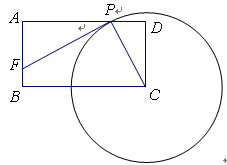
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
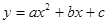 (
(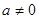 )的图象如图所示,有下列结论:⑴abc>0;⑵a+b+c>0;⑶a-b+c<0;其中正确的结论有( )
)的图象如图所示,有下列结论:⑴abc>0;⑵a+b+c>0;⑶a-b+c<0;其中正确的结论有( )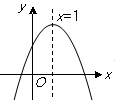
| A.0个 | B.1个 | C.2个 | D.3个 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com