
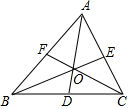
 如图,D、E、F分别为△ABC各边中点,AD、BE、CF交于O点,则图中面积相等的三角形共有( )
如图,D、E、F分别为△ABC各边中点,AD、BE、CF交于O点,则图中面积相等的三角形共有( )| A. | 15对 | B. | 18对 | C. | 30对 | D. | 33对 |
分析 分三种情况:面积为△ABC的$\frac{1}{2}$的三角形,面积为△ABC的$\frac{1}{6}$的三角形,面积为△ABC的$\frac{1}{3}$的三角形.
解答 解:△ABD、△ACD、△BCE、△BAE、△CAF、△CBF的面积相等,都是△ABC面积的$\frac{1}{2}$;
△OBD、△OCD、△OCE、△OAE、△OAF、△OBF的面积相等,都是△ABC面积的$\frac{1}{6}$;
△OAB、△OBC、△OAC的面积相等,都是△ABC面积的$\frac{1}{3}$.
共有33对.
故选:D.
点评 本题考查了三角形的面积,注意同底等高三角形面积的求法,等底等高三角形面积的求法,等底同高三角形面积的求法.


科目:初中数学 来源: 题型:填空题
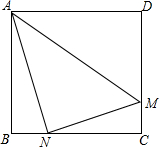 如图,折叠长方形ABCD,使顶点D与BC边上的N点重合,如果AD=7cm,DM=5cm,∠DAM=39°,则AN=7cm,NM=5cm,∠NAB=12°.
如图,折叠长方形ABCD,使顶点D与BC边上的N点重合,如果AD=7cm,DM=5cm,∠DAM=39°,则AN=7cm,NM=5cm,∠NAB=12°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
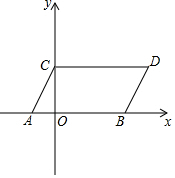 如图,在平面直角坐标系中,A(-1,0),B(3,0),C(0,2),CD∥x轴,CD=AB.
如图,在平面直角坐标系中,A(-1,0),B(3,0),C(0,2),CD∥x轴,CD=AB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系中,A,B,C三点的坐标分别为(-6,7),(-3,0),(0,3).
在平面直角坐标系中,A,B,C三点的坐标分别为(-6,7),(-3,0),(0,3).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
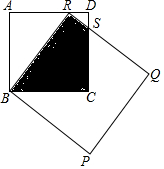 如图为两正方形ABCD,BPQR重叠的情形,其中R点在AD上,CD与QR相交于S点.若两正方形ABCD、BPQR的面积分别为16、25,则四边形RBCS的面积为何( )
如图为两正方形ABCD,BPQR重叠的情形,其中R点在AD上,CD与QR相交于S点.若两正方形ABCD、BPQR的面积分别为16、25,则四边形RBCS的面积为何( )| A. | 8 | B. | $\frac{17}{2}$ | C. | $\frac{28}{3}$ | D. | $\frac{77}{8}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com