
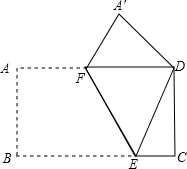
 如图,将矩形ABCD沿折痕FE对折,使点B与点D重合,点A落在点A′.
如图,将矩形ABCD沿折痕FE对折,使点B与点D重合,点A落在点A′.分析 (1)根据翻折变换的性质和矩形的性质得到∠A′DF=∠EDC,证明△A′FD≌△CDE;
(2)根据全等三角形的性质得到答案.
解答 (1)证明:∵AD∥BC,
∴∠DFE=∠FEB,又∠FEB=∠FED,
∴∠DEF=∠DFE,
∴DF=DE,
∵∠A′DE=∠B=90°,∠FDC=90°,
∴∠A′DF=∠EDC,
在△A′FD和△CDE中,
$\left\{\begin{array}{l}{∠A′=∠DEF}\\{∠A′DF=∠CDE}\\{DF=DE}\end{array}\right.$,
∴△A′FD≌△CDE;
(2)∵△A′FD≌△CDE,
∴A′F=CE.
点评 本题考查的是翻折变换的性质、全等三角形的判定和性质,找准翻折变换中的对应边和对应角是解题的关键,注意全等三角形的判定定理和性质定理的灵活运用.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
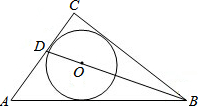 如图,⊙O是Rt△ABC的内切圆,∠C=90°,BO的延长线交BC于D,若BD=10,CD=6,则⊙O半径为$\frac{24}{7}$.
如图,⊙O是Rt△ABC的内切圆,∠C=90°,BO的延长线交BC于D,若BD=10,CD=6,则⊙O半径为$\frac{24}{7}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
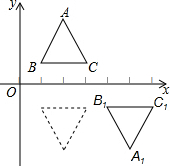 在平面直角坐标系中,把△ABC先沿x轴翻折,再向右平移3个单位得到△A1B1C1现把这两步操作规定为一种变换.如图,已知等边三角形ABC的顶点B、C的坐标分别是(1,1)、(3,1),把三角形经过连续5次这种变换得到三角形△A5B5C5,则点A的对应点A5的坐标是( )
在平面直角坐标系中,把△ABC先沿x轴翻折,再向右平移3个单位得到△A1B1C1现把这两步操作规定为一种变换.如图,已知等边三角形ABC的顶点B、C的坐标分别是(1,1)、(3,1),把三角形经过连续5次这种变换得到三角形△A5B5C5,则点A的对应点A5的坐标是( )| A. | (5,-$\sqrt{3}$) | B. | (14,1+$\sqrt{3}$) | C. | (17,-1-$\sqrt{3}$) | D. | (20,1+$\sqrt{3}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
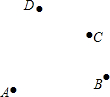 如图,平面上有A、B、C、D4个点,根据下列语句画图.
如图,平面上有A、B、C、D4个点,根据下列语句画图.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com