
 如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,过点B作射线BB1∥AC,动点D从点A出发沿射线AC方向以每秒5个单位的速度运动,同时动点E从点C出发,沿射线AC方向以每秒3个单位的速度运动,过点D作DH⊥AB于H,过点E作EF上AC交射线BB1于F,G是EF中点,连接DG,设点D运动的时间为t秒.
如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,过点B作射线BB1∥AC,动点D从点A出发沿射线AC方向以每秒5个单位的速度运动,同时动点E从点C出发,沿射线AC方向以每秒3个单位的速度运动,过点D作DH⊥AB于H,过点E作EF上AC交射线BB1于F,G是EF中点,连接DG,设点D运动的时间为t秒.分析 (1)先利用勾股定理求出AB=5,再用AD=AB建立方程求出t,即可得出结论;
(2)先求出GE,再分两种情况利用相似三角形得出的比例式建立方程求解即可;
(3)①先判断出△AHD∽△ACB得出比例式即可表示出AD=5t,AH=3t,DH=4t,再用等角的同名三角函数建立方程得出CO,即可AA',CC',OD,继而得出OH,即可得出结论;
②找出当线段A′C′与射线BB′,有公共点时的分界点,确定出分界点时的时间即可得出结论.
解答 解:(1)∵∠ACB=90°,AC=3,BC=4,
∴AB=5,
∴AD=5t,CE=3t,
当AD=AB时,5t=5,
∴t=1,
∴AE=AC+CE=3+3t=6,
∴DE=6-5=1;
(2)易得,四边形BCEF是矩形,
∴EF=BC=4,G是EF中点,
∴GE=2,
当AD<AE时,DE=AE-AD=3+3t-5t=3-2t,
当△DEG∽△ACB时,$\frac{DE}{AC}=\frac{EG}{BC}$,
∴$\frac{3-2t}{3}=\frac{2}{4}$,
∴t=$\frac{3}{4}$,
当△DEG∽△ACB时,$\frac{DE}{BC}=\frac{EG}{AC}$,
∴$\frac{3-2t}{4}=\frac{2}{3}$,
∴t=$\frac{1}{6}$,
即:当AD<AE时,若△DEG与△ACB相似,t的值为$\frac{3}{4}$或$\frac{1}{6}$;
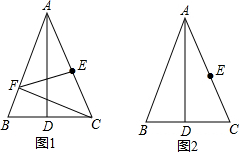
(3)①如图1,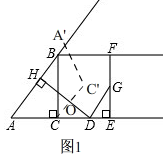
由轴对称得,AA'⊥DH,CC'⊥DH,AA'=2AH,CC'=2CO,
∵∠A=∠AA'C',∠AHD=∠ACB=90°,
∴△AHD∽△ACB,
∴$\frac{AH}{AC}=\frac{DH}{BC}=\frac{AD}{AB}$,
∴$\frac{AH}{3}=\frac{DH}{4}=\frac{AD}{5}$,
∵AD=5t,
∴AH=3t,DH=4t,
∵sin∠ADH=sin∠CDO,
∴$\frac{AH}{AD}=\frac{CO}{CD}$,
∴$\frac{3}{5}=\frac{CO}{5t-3}$,
∴CO=3t-$\frac{9}{5}$,
∴AA'=2AH=6t,CC'=2CO=6t-$\frac{18}{5}$,
∵OD=CD•cos∠CDO=(5t-3)×$\frac{4}{5}$=4t-$\frac{12}{5}$,
∴OH=DH-OD=$\frac{12}{5}$,
∴S=$\frac{1}{2}$(AA'+CC')•OH=$\frac{1}{2}$(6t+6t-$\frac{18}{5}$)=$\frac{72}{5}$t-$\frac{108}{25}$;
当点A'落在射线BB'上时,
如图2,连接BD,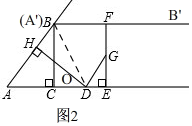 AA'=AB=5,
AA'=AB=5,
∴6t=5,
∴t=$\frac{5}{6}$,
当点C'落在射线BB'上时,
如图3,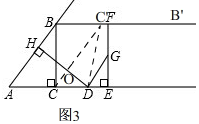
连接CC',DC',
易得,CC'∥AB,
∴四边形ACC'B是平行四边形,
∴CC'=AB=5,
∴6t-$\frac{18}{5}$=5,
∴t=$\frac{43}{30}$,
∴$\frac{5}{6}$≤t≤$\frac{43}{30}$.
点评 此题是相似形综合题,主要考查了矩形的判定和性质,相似三角形的判定的判断和性质,锐角三角函数的定义,平行四边形的判定和性质,梯形的面积公式,解(1)的关键是用AD=AB建立方程,解(2)的关键是分类讨论,解(3)的关键求出OH,是一道中考压轴题.


科目:初中数学 来源:2016~2017学年安徽省芜湖市九年级下学期第一次模拟考试数学试卷(解析版) 题型:解答题
如图1,在四边形ABCD中,∠DAB被对角线AC平分,且AC2=AB·AD,我们称该四边形为“可分四边形”,∠DAB称为“可分角”.
(1)如图2,四边形ABCD为“可分四边形”,∠DAB为“可分角”,如果∠DCB=∠DAB,则∠DAB=_________.
(2)如图3,在四边形ABCD中,∠DAB=60°,AC平分∠DAB,且∠BCD=150°,求证:四边形ABCD为“可分四边形”;
(3)现有四边形ABCD为“可分四边形”,∠DAB为“可分角”,且AC=4,BC=2,∠D=90°,求AD的长?

图1 图2 图3
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
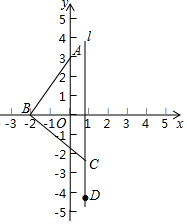 如图,已知在平面直角坐标系中,点A(0,3),点B为x轴上一动点,连接AB,线段AB绕着点B按顺时针方向旋转90°至线段CB,过点C作直线l∥y轴,在直线l上有一点D位于点C下方,满足CD=BO,则当点B从(-3,0)平移到(3,0)的过程中,点D的运动路径长为3+3$\sqrt{5}$.
如图,已知在平面直角坐标系中,点A(0,3),点B为x轴上一动点,连接AB,线段AB绕着点B按顺时针方向旋转90°至线段CB,过点C作直线l∥y轴,在直线l上有一点D位于点C下方,满足CD=BO,则当点B从(-3,0)平移到(3,0)的过程中,点D的运动路径长为3+3$\sqrt{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
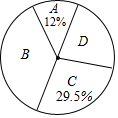 某区为了解七年级学生开展跳绳活动的情况,随机调查了该区部分学校七年级学生1分钟跳绳的次数,将调查结果进行统计,下面是根据调查数据制作的统计图表的一部分.
某区为了解七年级学生开展跳绳活动的情况,随机调查了该区部分学校七年级学生1分钟跳绳的次数,将调查结果进行统计,下面是根据调查数据制作的统计图表的一部分.| 分组 | 次数x(个) | 人数 |
| A | 0≤x<120 | 24 |
| B | 120≤x<130 | 72 |
| C | 130≤x<140 | |
| D | x≥140 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com