
【题目】如图,矩形ABCD中,AB=2cm,BC=6cm,把△ABC沿对角线AC折叠,得到△AB′C,且B′C与AD相交于点E,则AE的长为cm. 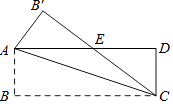
【答案】![]()
【解析】解:∵四边形ABCD是矩形, ∴AD∥BC,AD=BC=6cm,CD=AB=2cm,
∴∠ACB=∠DAC.
由折叠的性质得:∠ACB=∠ECA,
∴∠DAC=∠ECA.
∴AE=CE,
设AE=x,则CE=x,DE=6﹣x,
在Rt△CDE中,DE2+CD2=CE2 .
即(6﹣x)2+22=x2 ,
解得:x= ![]() .
.
即AE= ![]() ,
,
所以答案是: ![]() ,
,
【考点精析】本题主要考查了矩形的性质和翻折变换(折叠问题)的相关知识点,需要掌握矩形的四个角都是直角,矩形的对角线相等;折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等才能正确解答此题.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
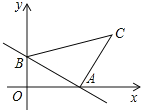
【题目】如图,一次函数y=﹣![]() x+3的图象分别与x轴、y轴交于点A、B,以线段AB为边在第一象限内作等腰Rt△ABC,∠BAC=90°,则过B、C两点直线的解析式是_____.
x+3的图象分别与x轴、y轴交于点A、B,以线段AB为边在第一象限内作等腰Rt△ABC,∠BAC=90°,则过B、C两点直线的解析式是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果商从批发市场用8000元购进了大樱桃和小樱桃各200千克,大樱桃的进价比小樱桃的进价每千克多20元.大樱桃售价为每千克40元,小樱桃售价为每千克16元.
(1)大樱桃和小樱桃的进价分别是每千克多少元?销售完后,该水果商共赚了多少元钱?
(2)该水果商第二次仍用8000元钱从批发市场购进了大樱桃和小樱桃各200千克,进价不变,但在运输过程中小樱桃损耗了20%.若小樱桃的售价不变,要想让第二次赚的钱不少于第一次所赚钱的90%,大樱桃的售价最少应为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD∥BC,AB∥CD,AC,BD交于O点,过O点的直线EF交AD于E点,交BC于F点,且BF=DE,则图中的全等三角形共有( )

A. 6对 B. 5对 C. 3对 D. 2对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一块长、宽、高分别为6cm、4cm、3cm的长方体木块,一只蚂蚁要从长方体木块的一个顶点A处,沿着长方体的表面到长方体上和A相对的顶点B处吃食物,那么它需要爬行的最短路径的长是( )

A. ![]() cm B.
cm B. ![]() cm C.
cm C. ![]() cm D. 9cm
cm D. 9cm
查看答案和解析>>
科目:初中数学 来源: 题型:
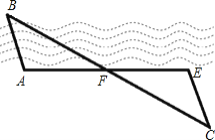
【题目】如图,小明和小月两家位于A,B两处隔河相望,要测得两家之间的距离,小明设计方案如下:
①从点A出发沿河岸画一条射线AM;
②在射线AM上截取AF=FE;
③过点E作EC∥AB,使B,F,C在一条直线上;
④CE的长就是A,B间的距离.
(1)请你说明小明设计的原理.
(2)如果不借助测量仪,小明的设计中哪一步难以实现?
(3)你能设计出更好的方案吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=90°,AB=5cm,BC=3cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒.
(1)出发2秒后,求△ABP的周长.
(2)问t为何值时,△BCP为等腰三角形?(要有必要的过程)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017湖北省鄂州市,第8题,3分)小东家与学校之间是一条笔直的公路,早饭后,小东步行前往学校,图中发现忘带画板,停下给妈妈打电话,妈妈接到电话后,带上画板马上赶往学校,同时小东沿原路返回,两人相遇后,小东立即赶往学校,妈妈沿原路返回16min到家,再过5min小东到达学校,小东始终以100m/min的速度步行,小东和妈妈的距离y(单位:m)与小东打完电话后的步行时间t(单位:min)之间的函数关系如图所示,下列四种说法:
①打电话时,小东和妈妈的距离为1400米;
②小东和妈妈相遇后,妈妈回家的速度为50m/min;
③小东打完电话后,经过27min到达学校;
④小东家离学校的距离为2900m.
其中正确的个数是( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】AD是△ABC的边BC上的中线,AB=12,AC=8,则边BC的取值范围是_______________________;中线AD的取值范围是__________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com