
【题目】已知二次函数y=2x2+4x-6.
(1)将其化成y=a(x-h)2+k的形式;
(2)写出开口方向,对称轴方程,顶点坐标;
(3)求图象与两坐标轴的交点坐标;
(4)画出函数图象;
(5)说明其图象与抛物线y=x2的关系;
(6)当x取何值时,y随x增大而减小;
(7)当x取何值时,y>0,y=0,y<0;
(8)当x取何值时,函数y有最值?其最值是多少?
(9)当y取何值时,-4<x<0;
(10)求函数图象与两坐标轴交点所围成的三角形面积.
【答案】(1)y=2(x+1)2-8;
(2)开口向上,直线x=-1,顶点(-1,-8);
(3)与x轴交点(-3,0)(1,0),与y轴交点(0,-6);
(4)图略;
(5)将抛物线y=x2向左平移1个单位,向下平移8个单位;然后图像上所有点横坐标扩大为原来的2倍,得到y=2x2+4x-6的图象;
(6)x≤-1;
(7)当x<-3或x>1时,y>0;当x=-3或x=1时,y=0;
当-3<x<1时,y<0;
(8)x=-1时,y最小值=-8;
(9)-8≤y<10;
(10)S△=12.
【解析】试题分析:(1)将函数表达式配方成顶点式形式,先将二次项、一次项分别提取a,然后加上![]() ,再减去
,再减去![]() 即可得到y=2(x+1)2-8.(2)由a值的正负,或图像可判断开口方向。顶点式可看出对称轴和顶点坐标。(3)分别让x=0,y=0可分别求出图像与y轴的坐标,和x轴的坐标.(4)可根据顶点坐标,图像与x、y轴交点坐标,简略画出函数图像.(5)将抛物线y=x2经过一定的平移可得到y=2(x+1)2-8.(6)根据函数图像可判断函数的增减性,最值以及x的取值与y.
即可得到y=2(x+1)2-8.(2)由a值的正负,或图像可判断开口方向。顶点式可看出对称轴和顶点坐标。(3)分别让x=0,y=0可分别求出图像与y轴的坐标,和x轴的坐标.(4)可根据顶点坐标,图像与x、y轴交点坐标,简略画出函数图像.(5)将抛物线y=x2经过一定的平移可得到y=2(x+1)2-8.(6)根据函数图像可判断函数的增减性,最值以及x的取值与y.
试题解析:(1)通过配方法可以将y=2x2+4x-6配方成y=2(x+1)2-8.
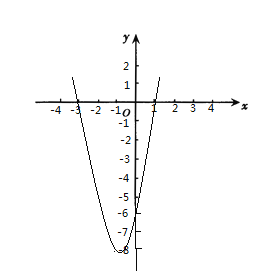
(2)由图像可以看出开口向上,由顶点式得对称轴为直线x=-1,顶点坐标为(-1,-8);
(3)当y=0时求得与x轴交点(-3,0)(1,0),可求得当x=0时与y轴交点(0,-6);
(4)如图所示为抛物线图像;(5)函数图像与抛物线y=x2的关系:观察图可知,是由抛物线y=x2先向左平移一个单位,然后图像上所有点横坐标扩大为原来的2倍,然后再向下平移八个单位得到的;(6)观察图,在对称轴左边,即x≤-1时,y随x的增大而减小。(7)有图得,x<-3或x>1时,y>0;当x=-3或x=1时,y=0;当-3<x<1时,y<0;(8)由图得,当x=-1时,y有最小值,y最小=-8;(9)当x=-4时,y=10;当x=0时,y=-8;所以,当-8≤y≤10时,-4≤x≤0;(10)函数图像与坐标轴交点坐标分别为(-3,0)、(1,0)、(0,-6),所以围成的三角形面积S=(3+1)×6×![]() =12.
=12.


 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:初中数学 来源: 题型:
【题目】下列运算正确的是( )
A.﹣a(a﹣b)=﹣a2﹣ab
B.2ab3a=6a2b
C.(2ab)2÷a2b=4ab
D.(a﹣1)(1﹣a)=a2﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠ABC和射线BD上一点P(点P与点B不重合,且点P到BA,BC的距离分别为PE,PF).

(1)若∠EBP=40°,∠FBP=20°,试比较PE,PF的大小;
(2)若∠EBP=α,∠FBP=β,α,β都是锐角,且α>β,请判断PE,PF的大小,并给出证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在![]() 中,
中, ![]() .过A点的直线
.过A点的直线![]() 从与边
从与边![]() 重合的位置开始绕点
重合的位置开始绕点![]() 按顺时针方向旋转角
按顺时针方向旋转角![]() ,直线
,直线![]() 交BC边于点
交BC边于点![]() (点
(点![]() 不与点
不与点![]() 、点
、点![]() 重合),
重合),![]() 的边
的边![]() 始终在直线
始终在直线![]() 上(点
上(点![]() 在点
在点![]() 的上方),且
的上方),且![]() ,连接
,连接![]() 。
。
(1)当![]() 时,
时,
①如图a,当![]() 时,求
时,求![]() 的度数;
的度数;
②如图b,当![]() 时,
时, ![]() 的度数是否发生变化?说明理由.
的度数是否发生变化?说明理由.
(2)如图c,当![]() 时,请直接写出
时,请直接写出![]() 与
与![]() 之间的数量关系,不必证明.
之间的数量关系,不必证明.
![]()

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com