
分析 利用求根公式,求出一元二次方程x2-x-1=0的根;利用配方的办法把m2-4m+5变形成( )2+正数的形式,再根据非负数的性质确定其最小值.
解答 解:因为x=$\frac{-b±\sqrt{{b}^{2}-4ac}}{2a}$
=$\frac{1±\sqrt{1+4}}{2}$
=$\frac{1±\sqrt{5}}{2}$
所以x1=$\frac{1+\sqrt{5}}{2}$,x2=$\frac{1-\sqrt{5}}{2}$.
m2-4m+5
=m2-4m+4+1
=(m-2)2+1
因为(m-2)2≥0
所以m2-4m+5的最小值是1
故答案为:x1=$\frac{1+\sqrt{5}}{2}$,x2=$\frac{1-\sqrt{5}}{2}$;1.
点评 本题考查了一元二次方程的解法、配方法个非负数的性质.方程ax2+bx+c=0的求根公式为:x=$\frac{-b±\sqrt{{b}^{2}-4ac}}{2a}$(2-4ac≥0),初中阶段接触的三种非负数是:$\sqrt{a}$,|a|,a2.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,四边形ABCD与ECGF是两个边长分别为a,b的正方形,
如图,四边形ABCD与ECGF是两个边长分别为a,b的正方形,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
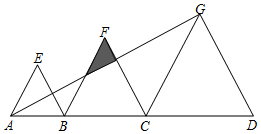 如图,点B、C是线段AD上的点,△ABE、△BCF、△CDG都是等边三角形,且AB=4,BC=6,已知△ABE与△CDG的相似比为2:5.则
如图,点B、C是线段AD上的点,△ABE、△BCF、△CDG都是等边三角形,且AB=4,BC=6,已知△ABE与△CDG的相似比为2:5.则查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com