已知圆的半径为13,两条弦长分别为10和24,且弦AB∥CD,则AB、CD相距 .
【答案】
分析:分两种情况考虑:(1)当两条弦在圆心O同侧时,如图1所示,过O作OE⊥CD,与AB交于F点,由AB∥CD,可得出OF⊥AB,连接OA,OC,利用垂径定理得到E、F分别为CD、AB的中点,由CD与AB的长求出CE与AF的长,再由半径OA与OC的长,利用勾股定理分别求出OE与OF,由OE-OF即可求出两弦间的距离EF的长;
(2)当两条弦在圆心O异侧时,如图1所示,过O作OE⊥CD,与AB交于F点,由AB∥CD,可得出OF⊥AB,连接OA,OC,利用垂径定理得到E、F分别为CD、AB的中点,由CD与AB的长求出CE与AF的长,再由半径OA与OC的长,利用勾股定理分别求出OE与OF,由OE+OF即可求出两弦间的距离EF的长,综上,得到AB与CD的距离.
解答:解:分两种情况考虑:
(1)当弦AB与弦CD在圆心O同侧时,如图1所示,
过O作OE⊥CD,与AB交于F点,由AB∥CD,可得出OF⊥AB,
连接OA,OC,
∵OE⊥CD,OF⊥AB,
∴E、F分别为CD、AB的中点,
∵AB=24,CD=10,
∴CE=DE=5,AF=BF=12,
又∵半径OA=OC=13,
∴在Rt△AOF中,根据勾股定理得:OF=
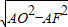
=5,
在Rt△COE中,根据勾股定理得:OE=
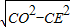
=12,
则两弦间的距离EF=OE-OF=12-5=7;
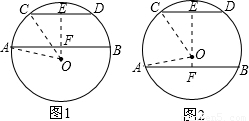
(2)当弦AB与弦CD在圆心O异侧时,如图2所示,
过O作OE⊥CD,与AB交于F点,由AB∥CD,可得出OF⊥AB,
连接OA,OC,
∵OE⊥CD,OF⊥AB,
∴E、F分别为CD、AB的中点,
∵AB=24,CD=10,
∴CE=DE=5,AF=BF=12,
又半径OA=OC=13,
∴在Rt△AOF中,根据勾股定理得:OF=
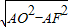
=5,
在Rt△COE中,根据勾股定理得:OE=
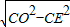
=12,
则两弦间的距离EF=OE+OF=12+5=17,
综上,两条弦间的距离为7或17.
故答案为:7或17.
点评:此题考查了垂径定理,以及勾股定理,利用了分类讨论的思想,分类讨论时要做到不重不漏.

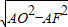 =5,
=5,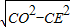 =12,
=12,
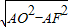 =5,
=5,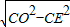 =12,
=12,

 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案