
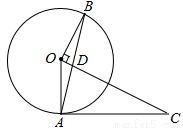
(7分)如图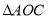 中,以
中,以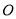 为圆心,
为圆心,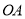 为半径作⊙
为半径作⊙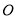 ,作
,作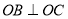 交⊙
交⊙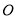 于点B,垂足为点
于点B,垂足为点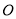 ,连接AB交
,连接AB交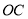 于点D,
于点D,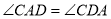 .
.
(1)求证:AC是⊙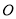 的切线;
的切线;
(2)若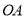 =5,
=5,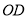 =1,求线段AC的长.
=1,求线段AC的长.
(1)证明略;(2)AC=12.
【解析】
试题分析:(1)根据已知条件“∠CAD=∠CDA”、对顶角∠BDO=∠CDA可以推知∠BDO=∠CAD;然后根据等腰三角形OAB的两个底角相等、直角三角形的两个锐角互余的性质推知,∠B+∠BDO=∠OAB+∠CAD=90°,即∠OAC=90°.所以线段AC是⊙O的切线;
(2)根据“等角对等边”可以推知AC=DC,所以由图形知OC=OD+CD;然后利用(1)中切线的性质可以在Rt△OAC中,根据勾股定理来求AC的长度.
试题解析:【解析】
(1)线段AC是⊙O的切线;
理由如下:∵∠CAD=∠CDA(已知),∠BDO=∠CDA(对顶角相等),
∴∠BDO=∠CAD(等量代换);
又∵OA=OB(⊙O的半径),
∴∠B=∠OAB(等边对等角);
∵OB⊥OC(已知),
∴∠B+∠BDO=∠OAB+∠CAD=90°,即∠OAC=90°,
∴线段AC是⊙O的切线;
(2)设AC=x(x>0).
∵∠CAD=∠CDA(已知),
∴DC=AC=x(等角对等边);
∵OA=5,OD=1,
∴OC=OD+DC=1+x;
∵由(1)知,AC是⊙O的切线,
∴在Rt△OAC中,根据勾股定理得,
OC2=AC2+OA2,即(1+x)2=x2+52,
解得x=12,即AC=12.
考点:1、勾股定理;2、切线的判定和性质.


科目:初中数学 来源:2014-2015学年福建省八年级上学期第三次监测数学试卷(解析版) 题型:解答题
(10分)甲、乙两重灾区急需一批大型挖掘机,甲地需25台,乙地需23台;A.B两省获知情况后慷慨相助,分别捐赠挖掘机26台和22台并将其全部调往灾区.若从A省调运一台挖掘机到甲地要耗资0.4万元,到乙地要耗资0.3万元;从B省调运一台挖掘机到甲地要耗资0.5万元,到乙地要耗资0.2万元.设从A省调往甲地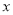 台,A.B两省将捐赠的挖掘机全部调往灾区共耗资y万元.
台,A.B两省将捐赠的挖掘机全部调往灾区共耗资y万元.
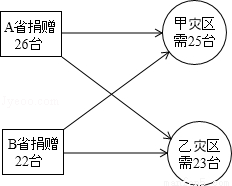
(1)求出y与x之间的函数关系式及自变量x的取值范围;
(2)若要使总耗资不超过15万元,有哪几种调运方案?
(3)怎样设计调运方案能使总耗资最少?最少耗资是多少万元?
查看答案和解析>>
科目:初中数学 来源:2014-2015学年福建省八年级上学期第三次监测数学试卷(解析版) 题型:选择题
若正比例函数的图像经过点(-1,2),则这个图像必经过点( )
A.(1,2) B.(-1,-2) C.(2,-1) D.(1,-2)
查看答案和解析>>
科目:初中数学 来源:2014-2015学年福建省八年级上学期第三次监测数学试卷(解析版) 题型:选择题
下列命题 :(1)绝对值最小的的实数不存在;(2)无理数在数轴上对应点不存在;(3)与本身的平方根相等的实数存在;(4)带根号的数都是无理数;(5)在数轴上与原点距离等于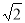 的点之间有无数多个点表示无理数,其中错误的命题的个数是( )
的点之间有无数多个点表示无理数,其中错误的命题的个数是( )
A.2 B.3 C.4 D.5
查看答案和解析>>
科目:初中数学 来源:2014-2015学年云南省腾冲县六校九年级上学期期末联考数学试卷(解析版) 题型:填空题
如图,在△ABC中,∠C=120°,AB=4cm,两等圆⊙A与⊙B外切,则图中两个扇形的面积之和(即阴影部分)为 cm2(结果保留π).
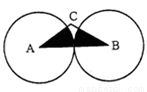
查看答案和解析>>
科目:初中数学 来源:2014-2015学年四川省九年级上学期期中考试数学试卷(解析版) 题型:选择题
如图是一个正方体的表面展开图,则原正方体中与“建”字所在的面相对的面上标的字是( )
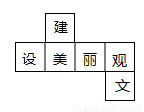
A. 美 B. 丽 C. 观 D. 文
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com