
”¾ĢāÄæ”æ2019ÄźĪŅŹ”æŖÕ¹ĮĖŅŌ”°øÄøļ““ŠĀ”¢·Ü·¢ÓŠĪŖ”±ĪŖÖ÷ĢāµÄ“óĢÖĀŪ»ī¶Æ£¬»ī¶Æ֊ijÉēĒųĪŖĮĖµ÷²é¾ÓĆń¶ŌÉēĒų·žĪńµÄĀśŅā¶Č£¬Ė껜³éČ”ĮĖÉēĒų²æ·Ö¾ÓĆń½ųŠŠĪŹ¾ķµ÷²é£»ÓĆ![]() ±ķŹ¾”°ŗÜĀśŅā”±£¬
±ķŹ¾”°ŗÜĀśŅā”±£¬![]() ±ķŹ¾”°ĀśŅā”±£¬
±ķŹ¾”°ĀśŅā”±£¬![]() ±ķŹ¾”°±Č½ĻĀśŅā”±£¬
±ķŹ¾”°±Č½ĻĀśŅā”±£¬![]() ±ķŹ¾”°²»ĀśŅā”±£¬ČēĶ¼ŹĒ¹¤×÷ČĖŌ±øł¾ŻĪŹ¾ķµ÷²éĶ³¼Ę׏ĮĻ»ęÖʵÄĮ½·ł²»ĶźÕūµÄĶ³¼ĘĶ¼.
±ķŹ¾”°²»ĀśŅā”±£¬ČēĶ¼ŹĒ¹¤×÷ČĖŌ±øł¾ŻĪŹ¾ķµ÷²éĶ³¼Ę׏ĮĻ»ęÖʵÄĮ½·ł²»ĶźÕūµÄĶ³¼ĘĶ¼.

ĒėÄćøł¾ŻĶ³¼ĘĶ¼Ģį¹©µÄŠÅĻ¢½ā“šŅŌĻĀĪŹĢā£ŗ
£Ø1£©±¾“ĪĪŹ¾ķµ÷²é¹²µ÷²éĮĖ¶ąÉŁøö¾ÓĆń£æ
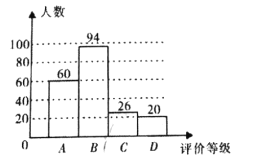
£Ø2£©Ēó³öµ÷²é½į¹ūĪŖ![]() µÄČĖŹż£¬²¢½«Ö±·½Ķ¼ÖŠ
µÄČĖŹż£¬²¢½«Ö±·½Ķ¼ÖŠ![]() ²æ·ÖµÄĶ¼ŠĪ²¹³äĶźÕū£»
²æ·ÖµÄĶ¼ŠĪ²¹³äĶźÕū£»
£Ø3£©Čē¹ūøĆÉēĒųÓŠ¾ÓĆń8000ČĖ£¬ĒėÄć¹Ą¼Ę¶ŌÉēĒų·žĪńøŠµ½”°²»ĀśŅā”±µÄ¾ÓĆńŌ¼ÓŠ¶ąÉŁČĖ£æ
”¾“š°ø”æ£Ø1£©200øö£»£Ø2£©![]() µÄČĖŹżÓŠ60ČĖ£¬Ķ¼¼ū½āĪö£»£Ø3£©800ČĖ.
µÄČĖŹżÓŠ60ČĖ£¬Ķ¼¼ū½āĪö£»£Ø3£©800ČĖ.
”¾½āĪö”æ
£Ø1£©±Č½ĻÖ±·½Ķ¼ŗĶÉČŠĪĶ¼µÄŠÅĻ¢£¬ÓĆCµČ¼¶µÄČĖŹż³żŅŌĖłÕ¼µÄ°Ł·Ö±ČæɵƵ÷²éµÄ×ÜČĖŹż£»
£Ø2£©ÓƵ÷²éµÄ×ÜČĖŹż³ĖŅŌAµČ¼¶µÄ°Ł·Ö±ČµĆµ½AµČ¼¶µÄČĖŹż£¬Č»ŗó²¹Č«Ö±·½Ķ¼£»
£Ø3£©ÓĆÉēĒų¾ÓĆńČĖŹż8000³ĖŅŌDµČ¼¶µÄ°Ł·Ö±ČæɵƓš°ø”£
½ā£ŗ£Ø1£©ÓÉĶ³¼ĘĶ¼æÉÖŖ£¬ĘĄ¼ŪµČ¼¶ĪŖ”°![]() ”±µÄČĖŹżĪŖ26ČĖ£¬Õ¼×ÜČĖŹżµÄ
”±µÄČĖŹżĪŖ26ČĖ£¬Õ¼×ÜČĖŹżµÄ![]() .
.
![]() £ØČĖ£©.
£ØČĖ£©.
“š£ŗ±¾“ĪĪŹ¾ķµ÷²é¹²µ÷²éĮĖ200øö¾ÓĆń.
£Ø2£©![]() £ØČĖ£©.
£ØČĖ£©.
“š£ŗµ÷²é½į¹ūĪŖ![]() µÄČĖŹżÓŠ60ČĖ.
µÄČĖŹżÓŠ60ČĖ.
²¹³äĶźÕūµÄÖ±·½Ķ¼ČēĶ¼ĖłŹ¾£ŗ
£Ø3£©![]() £ØČĖ£©.
£ØČĖ£©.
“š£ŗ¹Ą¼Ę¶ŌÉēĒų·žĪńøŠµ½”°²»ĀśŅā”±µÄ¾ÓĆńŌ¼ÓŠ800ČĖ.


 ÖĒ»ŪŠ”ø“Ļ°ĻµĮŠ“š°ø
ÖĒ»ŪŠ”ø“Ļ°ĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Å×ĪļĻß![]() £Øa”Ł0£©µÄ¶Ō³ĘÖįĪŖÖ±Ļßx=1£¬ÓėxÖįµÄŅ»øö½»µć×ų±źĪŖ£Ø©1£¬0£©£¬Ęä²æ·ÖĶ¼ĻóČēĶ¼ĖłŹ¾£¬ĻĀĮŠ½įĀŪ£ŗ
£Øa”Ł0£©µÄ¶Ō³ĘÖįĪŖÖ±Ļßx=1£¬ÓėxÖįµÄŅ»øö½»µć×ų±źĪŖ£Ø©1£¬0£©£¬Ęä²æ·ÖĶ¼ĻóČēĶ¼ĖłŹ¾£¬ĻĀĮŠ½įĀŪ£ŗ
¢Ł4ac£¼b2£»
¢Ś·½³Ģ![]() µÄĮ½øöøłŹĒx1=©1£¬x2=3£»
µÄĮ½øöøłŹĒx1=©1£¬x2=3£»
¢Ū3a+c£¾0
¢Üµ±y£¾0Ź±£¬xµÄȔֵ·¶Ī§ŹĒ©1”Üx£¼3
¢Żµ±x£¼0Ź±£¬yĖęxŌö“ó¶ųŌö“ó
ĘäÖŠ½įĀŪÕżČ·µÄøöŹżŹĒ£Ø””””£©

A. 4øö B. 3øö C. 2øö D. 1øö
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijÉĢ³”ĪŖĮĖĪüŅż¹ĖæĶ£¬ÉčĮ¢ĮĖŅ»øöæÉŅŌ×ŌÓÉ×Ŗ¶ÆµÄ×ŖÅĢ£¬ČēĶ¼ĖłŹ¾£¬²¢¹ę¶Ø£ŗ¹ĖæĶĻū·Ń200ŌŖ£Øŗ¬200ŌŖ£©ŅŌÉĻ£¬¾ĶÄÜ»ńµĆŅ»“Ī×Ŗ¶Æ×ŖÅĢµÄ»ś»į£¬Čē¹ū×ŖÅĢĶ£Ö¹ŗó£¬ÖøÕėÕżŗƶŌ×¼¾ÅÕŪ”¢°ĖÕŪ”¢ĘßÕŪĒųÓņ£¬¹ĖæĶ¾ĶæÉŅŌ»ńµĆ“ĖĻīÓÅ»Ż£¬Čē¹ūÖøÕėĒ”ŗĆŌŚ·ÖøīĻßÉĻŹ±£¬ŌņŠčÖŲŠĀ×Ŗ¶Æ×ŖÅĢ.
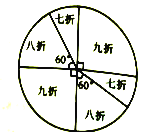
£Ø1£©Ä³¹ĖæĶÕżŗĆĻū·Ń220ŌŖ£¬Ėū×ŖŅ»“Ī×ŖÅĢ£¬Ėū»ńµĆ¾ÅÕŪ”¢°ĖÕŪ”¢ĘßÕŪÓÅ»ŻµÄøÅĀŹ·Ö±šŹĒ¶ąÉŁ£æ
£Ø2£©Ä³¹ĖæĶĻū·ŃÖŠ»ńµĆĮĖ×Ŗ¶ÆŅ»“Ī×ŖÅĢµÄ»ś»į£¬Źµ¼Źø¶·Ń168ŌŖ£¬ĒėĪŹĖūĻū·ŃĖł¹ŗĪļĘ·µÄŌ¼ŪÓ¦ĪŖ¶ąÉŁŌŖ.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĪŖĮĖČĆøü¶ąµÄŹ§Ń§¶łĶÆÖŲ·µŠ£Ō°£¬Ä³ÉēĒų×éÖÆ”°Ļ×°®ŠÄŹÖĄŹÖ”±¾čæī»ī¶Æ£¬¶ŌÉēĒų²æ·Ö¾čæī»§Źż½ųŠŠµ÷²éŗĶ·Ö×éĶ³¼Ęŗ󣬽«Źż¾ŻÕūĄķ³ÉČēĶ¼ĖłŹ¾µÄĶ³¼Ę±ķŗĶĶ³¼ĘĶ¼£ØĶ¼ÖŠŠÅĻ¢²»ĶźÕū£©£®ŅŃÖŖA”¢BĮ½×é¾čæī»§ŹżµÄ±ČĪŖ1£ŗ5£®
×鱚 | ¾čæī¶ī£Øx£©ŌŖ | »§Źż |
A | 1”Üx£¼50 | a |
B | 50”Üx£¼100 | 10 |
C | 100”Üx£¼150 | |
D | 150”Üx£¼200 | |
E | x”Ż200 |
Ēė½įŗĻŅŌÉĻŠÅĻ¢½ā“šĻĀĮŠĪŹĢā£®

£Ø1£©a= £¬±¾“Īµ÷²éŃł±¾µÄČŻĮæŹĒ £»
£Ø2£©²¹Č«”°¾čæī»§Źż·Ö×éĶ³¼Ę±ķŗĶ¾čæī»§ŹżĶ³¼ĘĶ¼1”±£»
£Ø3£©ČōøĆÉēĒųÓŠ1500»§×”»§£¬Ēėøł¾ŻŅŌÉĻŠÅĻ¢¹Ą¼Ę£¬Č«ÉēĒų¾čæī²»ÉŁÓŚ150ŌŖµÄ»§ŹżŹĒ¶ąÉŁ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĪŖĮĖ½āijŠ£Ń§ÉśµÄÉķøßĒéæö£¬ĶõĄĻŹ¦Ė껜³éČ”øĆŠ£ÄŠÉś”¢Å®Éś½ųŠŠ³éŃłµ÷²é£¬ŅŃÖŖ³éČ”µÄŃł±¾ÖŠ£¬ÄŠÉś”¢Å®ÉśČĖŹżĻąĶ¬£¬ĄūÓĆĖłµĆŹż¾Ż»ęÖĘČēĻĀĶ³¼ĘĶ¼±ķ£ŗ
×鱚 | Éķøß |
|
|
|
|
|
|
|
|
|
|
ÉķøßĒéæö·Ö×é±ķ
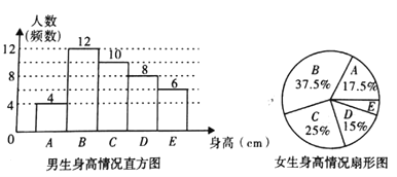
øł¾ŻĶ¼±ķĢį¹©µÄŠÅĻ¢£¬»Ų“šĻĀĮŠĪŹĢā£ŗ
£Ø1£©Ńł±¾ÖŠ£¬Å®ÉśÉķøßŌŚ![]() ×éµÄČĖŹżÓŠ_________ČĖ£»
×éµÄČĖŹżÓŠ_________ČĖ£»
£Ø2£©ŌŚÉĻĆęµÄÉČŠĪĶ³¼ĘĶ¼ÖŠ£¬±ķŹ¾![]() ×éµÄÉČŠĪµÄŌ²ŠÄ½ĒŹĒ_________”ć£»
×éµÄÉČŠĪµÄŌ²ŠÄ½ĒŹĒ_________”ć£»
£Ø3£©ŅŃÖŖøĆŠ£¹²ÓŠÄŠÉś800ČĖ£¬Å®Éś760ČĖ£¬Ēė¹Ą¼ĘøĆŠ£ÉķøßŌŚ![]() Ö®¼äµÄѧɜŌ¼ÓŠ¶ąÉŁČĖ£æ
Ö®¼äµÄѧɜŌ¼ÓŠ¶ąÉŁČĖ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬”ĻACB=90”ć£¬µćD£¬E·Ö±šŹĒ±ßBC£¬ABÉĻµÄÖŠµć£¬Į¬½ÓDE²¢ŃÓ³¤ÖĮµćF£¬Ź¹EF=2DF£¬Į¬½ÓCE”¢AF£®
£Ø1£©Ö¤Ć÷£ŗAF=CE£»
£Ø2£©µ±”ĻB=30”揱£¬ŹŌÅŠ¶ĻĖıߊĪACEFµÄŠĪד²¢ĖµĆ÷ĄķÓÉ£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼1£¬ŌŚ![]() ÖŠ£¬
ÖŠ£¬ ![]() £¬
£¬ ![]() .µćOŹĒBCµÄÖŠµć£¬µćDŃŲB”śA”śC·½Ļņ“ÓBŌĖ¶Æµ½C£®ÉčµćD¾¹żµÄĀ·¾¶³¤ĪŖ
.µćOŹĒBCµÄÖŠµć£¬µćDŃŲB”śA”śC·½Ļņ“ÓBŌĖ¶Æµ½C£®ÉčµćD¾¹żµÄĀ·¾¶³¤ĪŖ![]() £¬Ķ¼1֊ijĢõĻ߶ĪµÄ³¤ĪŖy£¬Čō±ķŹ¾yÓėxµÄŗÆŹż¹ŲĻµµÄ“óÖĀĶ¼ĻóČēĶ¼2ĖłŹ¾£¬ŌņÕāĢõĻ߶ĪæÉÄÜŹĒĶ¼1ÖŠµÄ£Ø””””£©
£¬Ķ¼1֊ijĢõĻ߶ĪµÄ³¤ĪŖy£¬Čō±ķŹ¾yÓėxµÄŗÆŹż¹ŲĻµµÄ“óÖĀĶ¼ĻóČēĶ¼2ĖłŹ¾£¬ŌņÕāĢõĻ߶ĪæÉÄÜŹĒĶ¼1ÖŠµÄ£Ø””””£©

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĶźČ«Ę½·½¹«Ź½£ŗ£Øa”Ąb£©2£½a2”Ą2ab+b2ŹŹµ±µÄ±äŠĪ£¬æÉŅŌ½ā¾öŗܶąµÄŹżŃ§ĪŹĢā£®
ĄżČē£ŗČōa+b£½3£¬ab£½1£¬Ēóa2+b2µÄÖµ£®
½ā£ŗŅņĪŖa+b£½3£¬ab£½1
ĖłŅŌ£Øa+b£©2£½9£¬2ab£½2
ĖłŅŌa2+b2+2ab£½9£¬2ab£½2
µĆa2+b2£½7
øł¾ŻÉĻĆęµÄ½āĢāĖ¼Ā·Óė·½·Ø£¬½ā¾öĻĀĮŠĪŹĢā£ŗ
£Ø1£©Čō£Ø7©x£©£Øx©4£©£½1£¬Ēó£Ø7©x£©2+£Øx©4£©2µÄÖµ£»
£Ø2£©ČēĶ¼£¬µćCŹĒĻ߶ĪABÉĻµÄŅ»µć£¬ŅŌAC”¢BCĪŖ±ßĻņĮ½±ß×÷Õż·½ŠĪ£¬ÉčAB£½5£¬Į½Õż·½ŠĪµÄĆ껿ŗĶS1+S2£½17£¬ĒóĶ¼ÖŠŅõÓ°²æ·ÖĆ껿£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬µćOŹĒ”÷ABCÄŚŅ»µć£¬Į¬½įOB”¢OC£¬²¢½«AB”¢OB”¢OC”¢ACµÄÖŠµćD”¢E”¢F”¢GŅĄ“ĪĮ¬½į£¬µĆµ½ĖıߊĪDEFG£®

£Ø1£©ĒóÖ¤£ŗĖıߊĪDEFGŹĒĘ½ŠŠĖıߊĪ£»
£Ø2£©Čē¹ū”ĻOBC=45”ć£¬”ĻOCB=30”ć£¬OC=4£¬ĒóEFµÄ³¤£®
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com