
分析 先根据题意列出不等式,再根据求不等式的基本性质求出不等式的解集.
解答 解:由题意得$\frac{3k-2}{5}$≤$\frac{2k+1}{3}$-1,
3(3k-2)≤5(2k+1)-15,
9k-6≤10k+5-15,
-k≤-4,
k≥4.
故当k≥4时,若代数式$\frac{3k-2}{5}$的值不大于代数式$\frac{2k+1}{3}$-1的值.
点评 本题考查了同学们解简单不等式的能力,解答这类题学生往往在解题时不注意移项要改变符号这一点而出错.解不等式要依据不等式的基本性质,在不等式的两边同时加上或减去同一个数或整式不等号的方向不变;在不等式的两边同时乘以或除以同一个正数不等号的方向不变;在不等式的两边同时乘以或除以同一个负数不等号的方向改变.


 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:初中数学 来源: 题型:解答题
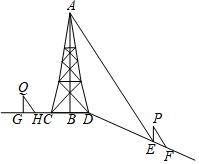 如图,在斜坡顶部有一铁塔AB,B是CD的中点,CD是水平的.在阳光的照射下,塔影DE留在斜坡面上.在同一时刻,小明站在点E处,其影子EF在直线DE上,小华站在点G处,影子GH在直线CD上,他们的影子长分别为2m和1m.已知CD=12m,DE=18m,小明和小华身高均为1.6m,那么塔高AB为多少?
如图,在斜坡顶部有一铁塔AB,B是CD的中点,CD是水平的.在阳光的照射下,塔影DE留在斜坡面上.在同一时刻,小明站在点E处,其影子EF在直线DE上,小华站在点G处,影子GH在直线CD上,他们的影子长分别为2m和1m.已知CD=12m,DE=18m,小明和小华身高均为1.6m,那么塔高AB为多少?查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
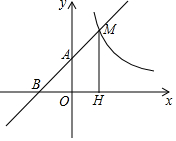 如图,直线y=x+1与x轴交于点B,y轴交于A点,与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点M,过M作MH⊥x轴于点H,且AO=$\frac{1}{2}$MH.
如图,直线y=x+1与x轴交于点B,y轴交于A点,与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点M,过M作MH⊥x轴于点H,且AO=$\frac{1}{2}$MH.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com