
ЁОЬтФПЁПжиЧьЪаЕФжиДѓЛнУёЙЄГЬЉЉЙЋзтЗПНЈЩшвбТНајПЂЙЄЃЌМЦЛЎ10ФъФкНтОіЕЭЪеШыШЫШКЕФзЁЗПЮЪЬтЃЌЧА6ФъЃЌУПФъПЂЙЄЭЖШыЪЙгУЕФЙЋзтЗПУцЛ§yЃЈЕЅЮЛЃКАйЭђЦНЗНУзЃЉЃЌгыЪБМфxЕФЙиЯЕЪЧy=![]() x+5ЃЌЃЈxЕЅЮЛЃКФъЃЌ1ЁмxЁм6ЧвxЮЊећЪ§ЃЉЃЛКѓ4ФъЃЌУПФъПЂЙЄЭЖШыЪЙгУЕФЙЋзтЗПУцЛ§yЃЈЕЅЮЛЃКАйЭђЦНЗНУзЃЉЃЌгыЪБМфxЕФЙиЯЕЪЧy=-
x+5ЃЌЃЈxЕЅЮЛЃКФъЃЌ1ЁмxЁм6ЧвxЮЊећЪ§ЃЉЃЛКѓ4ФъЃЌУПФъПЂЙЄЭЖШыЪЙгУЕФЙЋзтЗПУцЛ§yЃЈЕЅЮЛЃКАйЭђЦНЗНУзЃЉЃЌгыЪБМфxЕФЙиЯЕЪЧy=-![]() x+
x+![]() ЃЈxЕЅЮЛЃКФъЃЌ7ЁмxЁм10ЧвxЮЊећЪ§ЃЉЃЎМйЩшУПФъЕФЙЋзтЗПШЋВПГізтЭъЃЎСэЭтЃЌЫцзХЮяМлЩЯеЧЕШвђЫиЕФгАЯьЃЌУПФъЕФзтН№вВЫцжЎЩЯЕїЃЌдЄМЦЃЌЕкxФъЭЖШыЪЙгУЕФЙЋзтЗПЕФзтН№zЃЈЕЅЮЛЃКдЊ/m2ЃЉгыЪБМфxЃЈЕЅЮЛЃКФъЃЌ1ЁмxЁм10ЧвxЮЊећЪ§ЃЉТњзувЛДЮКЏЪ§ЙиЯЕШчЯТБэЃК
ЃЈxЕЅЮЛЃКФъЃЌ7ЁмxЁм10ЧвxЮЊећЪ§ЃЉЃЎМйЩшУПФъЕФЙЋзтЗПШЋВПГізтЭъЃЎСэЭтЃЌЫцзХЮяМлЩЯеЧЕШвђЫиЕФгАЯьЃЌУПФъЕФзтН№вВЫцжЎЩЯЕїЃЌдЄМЦЃЌЕкxФъЭЖШыЪЙгУЕФЙЋзтЗПЕФзтН№zЃЈЕЅЮЛЃКдЊ/m2ЃЉгыЪБМфxЃЈЕЅЮЛЃКФъЃЌ1ЁмxЁм10ЧвxЮЊећЪ§ЃЉТњзувЛДЮКЏЪ§ЙиЯЕШчЯТБэЃК
zЃЈдЊ/m2ЃЉ | 50 | 52 | 54 | 56 | 58 | Ё |
xЃЈФъЃЉ | 1 | 2 | 3 | 4 | 5 | Ё |
ЃЈ1ЃЉЧѓГіzгыxЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ2ЃЉЧѓеўИЎдкЕкМИФъЭЖШыЕФЙЋзтЗПЪеШЁЕФзтН№зюЖрЃЌзюЖрЮЊЖрЩйАйЭђдЊЃЛ
ЃЈ3ЃЉШєЕк6ФъПЂЙЄЭЖШыЪЙгУЕФЙЋзтЗППЩНтОі20ЭђШЫЕФзЁЗПЮЪЬтЃЌеўИЎМЦЛЎдкЕк10ФъЭЖШыЕФЙЋзтЗПзмУцЛ§ВЛБфЕФЧщПіЯТЃЌвЊШУШЫОљзЁЗПУцЛ§БШЕк6ФъШЫОљзЁЗПУцЛ§ЬсИпa%ЃЌетбљПЩНтОізЁЗПЕФШЫЪ§НЋБШЕк6ФъМѕЩй1.35a%ЃЌЧѓaЕФжЕЃЎ
ЃЈВЮПМЪ§ОнЃК![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЉ
ЃЉ
ЁОД№АИЁПЃЈ1ЃЉz=2x+48ЃЈ2ЃЉЕк3ФъЪеШЁЕФзтН№зюЖрЃЌзюЖрЮЊ243АйЭђдЊЃЈ3ЃЉaЕФжЕЮЊ20
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉЩшz=kx+bЃЈkЁй0ЃЉЃЌШЛКѓАбБэИёжаЕФСНзщЪ§ОнДњШыНтЮіЪНЃЌНтЗНГЬзщМДПЩЃЛЃЈ2ЃЉЩшЪеШЁЕФзтН№ЮЊWАйЭђдЊЃЌЗжБ№ЧѓГіЕБ1ЁмxЁм6ЪБКЭЕБ7ЁмxЁм10ЪБЕФWгыxЕФКЏЪ§ЙиЯЕЪНЃЌШЛКѓЗжБ№ЧѓГіСНИіКЏЪ§ЕФзюДѓжЕЃЌБШНЯДѓаЁЃЌПЩШЗЖЈЪеШЁЕФзтН№ЕФзюДѓжЕЃЛЃЈ3ЃЉЯШЧѓГіЕк6ФъКЭЕк10ФъЕФЭЖШыЪЙгУЕФЙЋзтЗПУцЛ§ЃЌШЛКѓИљОнЬтвтСаЗНГЬЕУЃК20ЁСЃЈ1-1ЃЎ35aЃЅЃЉЁС20ЁСЃЈ1+aЃЅЃЉ=350ЃЌШЛКѓНтЗНГЬМДПЩЃЎ
ЪдЬтНтЮіЃКНтЃКЃЈ1ЃЉгЩЬтвтЃЌzгыxГЩвЛДЮКЏЪ§ЙиЯЕЃЌ
Щшz=kx+bЃЈkЁй0ЃЉЃЎАбЃЈ1ЃЌ50ЃЉЃЎЃЈ2ЃЌ52ЃЉДњШыЃЌ
ЕУ![]() Ёрz=2x+48ЃЎ ЃЈ2ЗжЃЉ
Ёрz=2x+48ЃЎ ЃЈ2ЗжЃЉ
ЃЈ2ЃЉЕБ1ЁмxЁм6ЪБЃЌЩшЪеШЁЕФзтН№ЮЊW1АйЭђдЊЃЌдђ
W1=ЃЈ-![]() x+5ЃЉЃЈ2x+48ЃЉ
x+5ЃЉЃЈ2x+48ЃЉ
=-![]() x2+2x+240ЃЌ
x2+2x+240ЃЌ
ЁпЖдГЦжсx=-![]() Ёй=3ЃЌЖј1ЁмxЁм6ЃЌ
Ёй=3ЃЌЖј1ЁмxЁм6ЃЌ
ЁрЕБx=3ЪБЃЌW1зюДѓ=243ЃЈАйЭђдЊЃЉЃЎ
ЕБ7ЁмxЁм10ЪБЃЌЩшЪеШЁЕФзтН№ЮЊW2АйЭђдЊЃЌдђ
W2=ЃЈ-![]() x+
x+![]() ЃЉЁЄЃЈ2x+48ЃЉ
ЃЉЁЄЃЈ2x+48ЃЉ
=-![]() x2+
x2+![]() x+228ЃЎ
x+228ЃЎ
ЁпЖдГЦжсx=-![]() =7ЃЌЖј7ЁмxЁм10ЃЌ
=7ЃЌЖј7ЁмxЁм10ЃЌ
ЁрЕБx=7ЪБЃЌW2зюДѓ=![]() ЃЈАйЭђдЊЃЉЃЎ
ЃЈАйЭђдЊЃЉЃЎ
Ёп243>![]() ЃЌ
ЃЌ
ЁрЕк3ФъЪеШЁЕФзтН№зюЖрЃЌзюЖрЮЊ243АйЭђдЊЃЎ ЃЈ6ЗжЃЉ
ЃЈ3ЃЉЕБx=6ЪБЃЌ
y=-![]() ЁС6+5=4АйЭђЦНЗНУз=400ЭђЦНЗНУзЃЛ
ЁС6+5=4АйЭђЦНЗНУз=400ЭђЦНЗНУзЃЛ
ЕБx=10ЪБЃЌ
y=-![]() ЁС10+
ЁС10+![]() =3ЃЎ5АйЭђЦНЗНУз=350ЭђЦНЗНЃЎ
=3ЃЎ5АйЭђЦНЗНУз=350ЭђЦНЗНЃЎ
ЁпЕк6ФъПЩНтОі20ЭђШЫзЁЗПЮЪЬтЃЌ
ЁрШЫОљзЁЗПЮЊ400ЁТ20=20ЦНЗНУзЃЎ
гЩЬтвт20ЁСЃЈ1-1ЃЎ35aЃЅЃЉЁС20ЁСЃЈ1+aЃЅЃЉ=350ЃЎ
ЩшaЃЅ=mЃЌЛЏМђЮЊ54m2+14m-5=0ЃЌ
ІЄ=142-4ЁС54ЁСЃЈ-5ЃЉ=1276ЃЌ
Ёрm=![]()
Ёп![]() Ёж17ЃЎ8ЃЌЁрm1=0ЃЎ2ЃЌm2=-
Ёж17ЃЎ8ЃЌЁрm1=0ЃЎ2ЃЌm2=-![]() ЃЈВЛЗћЬтвтЃЌЩсШЅЃЉЃЎ
ЃЈВЛЗћЬтвтЃЌЩсШЅЃЉЃЎ
ЁрaЃЅ=0ЃЎ2ЃЌЁрa=20ЃЎ
Д№ЃКaЕФжЕЮЊ20ЃЎ ЃЈ10ЗжЃЉ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
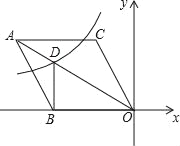
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌСтаЮABOCЕФЖЅЕуOдкзјБъдЕуЃЌБпBOдкxжсЕФИКАыжсЩЯЃЌЁЯBOC=60ЁуЃЌЖЅЕуCЕФзјБъЮЊЃЈmЃЌ3![]() ЃЉЃЌЗДБШР§КЏЪ§y=
ЃЉЃЌЗДБШР§КЏЪ§y=![]() ЕФЭМЯѓгыСтаЮЖдНЧЯпAOНЛгкЕуDЃЌСЌНгBDЃЌЕБBDЁЭxжсЪБЃЌkЕФжЕЪЧ_____ЃЎ
ЕФЭМЯѓгыСтаЮЖдНЧЯпAOНЛгкЕуDЃЌСЌНгBDЃЌЕБBDЁЭxжсЪБЃЌkЕФжЕЪЧ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЯрСкСНЕуОрРыЮЊ1ЕФЕуеѓжНЩЯЃЈзѓгвЯрСкЛђЩЯЯТЯрСкЕФСНЕужЎМфЕФОрРыЖМЪЧ1ИіЕЅЮЛГЄЖШЃЉЃЌШ§ИіЖЅЕуЖМдкЕуеѓЩЯЕФШ§НЧаЮНазіЕуеѓШ§НЧаЮЃЌЧыАДвЊЧѓЭъГЩЯТСаВйзїЃК

ЃЈ1ЃЉНЋЕуеѓЁїABCЫЎЦНЯђгвЦНвЦ4ИіЕЅЮЛГЄЖШЃЌдйЪњжБЯђЩЯЦНвЦ5ИіЕЅЮЛГЄЖШЃЌЛГіЦНвЦКѓЕФЁїA1B1C1ЃЛ
ЃЈ2ЃЉСЌНгAA1ЁЂBB1ЃЌдђЯпЖЮAA1ЁЂBB1ЕФЮЛжУЙиЯЕЮЊЁЁ ЁЂЪ§СПЙиЯЕЮЊЁЁ ЃЎЙРМЦЯпЖЮAA1ЕФГЄЖШДѓдМдкЁЁ ЃМAA1ЃМЁЁ ЕЅЮЛГЄЖШЃКЃЈЬюаДСНИіЯрСкећЪ§ЃЉЃЛ
ЃЈ3ЃЉЛГіЁїABCБпABЩЯЕФИпCDЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
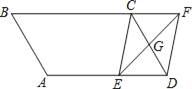
ЁОЬтФПЁПШчЭМЃЌABCDжаЃЌGЪЧCDЕФжаЕуЃЌEЪЧБпГЄADЩЯЕФЖЏЕуЃЌEGЕФбгГЄЯпгыBCЕФбгГЄЯпЯрНЛгкЕуFЃЌСЌНгCEЃЌDFЃЎ
ЃЈ1ЃЉЧѓжЄЃКЫФБпаЮCEDFЪЧЦНааЫФБпаЮЃЎ
ЃЈ2ЃЉЬюПеЃКШєABЃН3cmЃЌBCЃН5cmЃЌЁЯBЃН60ЁуЃЌдђЂйЕБAEЃНЁЁ ЁЁЪБЃЌЫФБпаЮCEDFЪЧОиаЮЃЛЂкЕБAEЃНЁЁ ЁЁЪБЃЌЫФБпаЮCEDFЪЧСтаЮЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
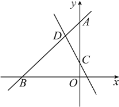
ЁОЬтФПЁПШчЭМЃЌжБЯпyЃНkxЃЋ4(kЁй0)гыxжсЁЂyжсЗжБ№НЛгкЕуBЃЌAЃЌжБЯпyЃНЃ2xЃЋ1гыyжсНЛгкЕуCЃЌгыжБЯпyЃНkxЃЋ4НЛгкЕуDЃЌЁїACDЕФУцЛ§ЪЧ![]() .
.
(1)ЧѓжБЯпABЕФБэДяЪНЃЛ
(2)ЩшЕуEдкжБЯпABЩЯЃЌЕБЁїACEЪЧжБНЧШ§НЧаЮЪБЃЌЧыжБНгаДГіЕуEЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
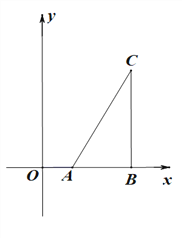
ЁОЬтФПЁПвбжЊAЃЈ2,0ЃЉЃЌBЃЈ6,0ЃЉЃЌCBЁЭxжсгкЕуBЃЌСЌНгAC
ЛЭМВйзїЃК
ЃЈ1ЃЉдкyе§АыжсЩЯЧѓзїЕуPЃЌЪЙЕУЁЯAPB=ЁЯACBЃЈГпЙцзїЭМЃЌБЃСєзїЭМКлМЃЃЉ
РэНтгІгУЃК
ЃЈ2ЃЉдкЃЈ1ЃЉЕФЬѕМўЯТЃЌ
ЂйШєtanЁЯAPB ![]() ЃЌЧѓЕуPЕФзјБъ
ЃЌЧѓЕуPЕФзјБъ
ЂкЕБЕуPЕФзјБъЮЊ ЪБЃЌЁЯAPBзюДѓ
ЭиеЙбгЩьЃК
ЃЈ3ЃЉШєдкжБЯпy![]() x+4ЩЯДцдкЕуPЃЌЪЙЕУЁЯAPBзюДѓЃЌЧѓЕуPЕФзјБъ
x+4ЩЯДцдкЕуPЃЌЪЙЕУЁЯAPBзюДѓЃЌЧѓЕуPЕФзјБъ
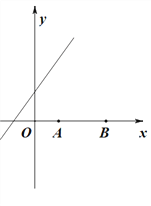
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌDЮЊABБпЩЯвЛЕуЃЌEЮЊCDжаЕуЃЌAC=![]() ЃЌЁЯABC=30ЁуЃЌЁЯA=ЁЯBED=45ЁуЃЌдђBDЕФГЄЮЊЃЈЁЁЁЁЃЉ
ЃЌЁЯABC=30ЁуЃЌЁЯA=ЁЯBED=45ЁуЃЌдђBDЕФГЄЮЊЃЈЁЁЁЁЃЉ

A. ![]() B.
B. ![]() +1Љ
+1Љ![]() C.
C. ![]() Љ
Љ![]() D.
D. ![]() Љ1
Љ1
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
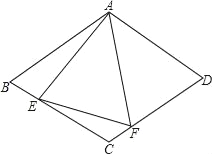
ЁОЬтФПЁПШчЭМЃЌдкСтаЮABCDжаЃЌAB=4ЃЌЁЯBAD=120ЁуЃЌЁїAEFЮЊе§Ш§НЧаЮЃЌEЁЂFдкСтаЮЕФБпBCЃЌCDЩЯЃЎ
ЃЈ1ЃЉжЄУїЃКBE=CFЃЎ
ЃЈ2ЃЉЕБЕуEЃЌFЗжБ№дкБпBCЃЌCDЩЯвЦЖЏЪБЃЈЁїAEFБЃГжЮЊе§Ш§НЧаЮЃЉЃЌЧыЬНОПЫФБпаЮAECFЕФУцЛ§ЪЧЗёЗЂЩњБфЛЏЃПШєВЛБфЃЌЧѓГіетИіЖЈжЕЃЛШчЙћБфЛЏЃЌЧѓГіЦфзюДѓжЕЃЎ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЧщПіЯТЃЌЧыЬНОПЁїCEFЕФУцЛ§ЪЧЗёЗЂЩњБфЛЏЃПШєВЛБфЃЌЧѓГіетИіЖЈжЕЃЛШчЙћБфЛЏЃЌЧѓГіЦфзюДѓжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕ![]() жаЃЌКЏЪ§
жаЃЌКЏЪ§![]() ЕФЭМЯѓгыжБЯп
ЕФЭМЯѓгыжБЯп![]() НЛгкЕуA(3,m).
НЛгкЕуA(3,m).
ЃЈ1ЃЉЧѓkЁЂmЕФжЕЃЛ
ЃЈ2ЃЉвбжЊЕуP(nЃЌn)(n>0)ЃЌЙ§ЕуPзїЦНаагк![]() жсЕФжБЯпЃЌНЛжБЯпy=x-2гкЕуMЃЌЙ§ЕуPзїЦНаагкyжсЕФжБЯпЃЌНЛКЏЪ§
жсЕФжБЯпЃЌНЛжБЯпy=x-2гкЕуMЃЌЙ§ЕуPзїЦНаагкyжсЕФжБЯпЃЌНЛКЏЪ§![]() ЕФЭМЯѓгкЕуN.
ЕФЭМЯѓгкЕуN.
ЂйЕБn=1ЪБЃЌХаЖЯЯпЖЮPMгыPNЕФЪ§СПЙиЯЕЃЌВЂЫЕУїРэгЩЃЛ
ЂкШєPNЁнPMЃЌНсКЯКЏЪ§ЕФЭМЯѓЃЌжБНгаДГіnЕФШЁжЕЗЖЮЇ.

ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com