有一个二次函数的图象,三位学生分别说出了它的一些特点.
甲:对称轴是直线x=4;
乙:与x轴两交点的横坐标都是整数;
丙:与y轴交点的纵坐标也是整数,且以这三个交点为顶点的三角形面积为3;
请写出满足上述全部特点的二次函数解析式.
解:此题答案不唯一
设所求解析式为y=a(x-x
1)(x-x
2),(其中x
1<x
2),则
其图象与x轴两交点分别是A(x
1,0),B(x
2,0),与y轴交点坐标是(0,ax
1x
2).
因为交点式a(x-x
1)(x-x
2),
又因为与y轴交点的横坐标为0,
所以a(0+x
1)(0+x
2),也就是ax
1x
2,
∵抛物线对称轴是直线x=4,
∴x
2-4=4-x
1,即:x
1+x
2=8 ①
∵S△ABC=3,∴(x
2-x
1)•|ax
1x
2|=6,即:x
2-x
1=

②
①②两式相加减,可得:x2=4+
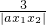
,
x
1=4-
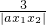
,
∵x
1,x
2是整数,ax
1x
2也是整数,
∴ax
1x
2是3的约数,共可取值为:±1,±3.
当ax
1x
2=±1时,x
2=7,x
1=1,a=±

当ax
1x
2=±3时,x
2=5,x1=
3,a=±

因此,所求解析式为:y=±

(x-7)(x-1)或y=±

(x-5)(x-3)
即:y
1=

x
2-

x+1,
y
2=-

x
2+

x-1.
y
3=

x
2-

x+3,
y
4=-

x
2+

x-3.
故答案为:y=

x
2-

x+3(答案不唯一).
分析:由对称轴是直线x=4,与x轴两交点的横坐标都是整数,可设与x轴两交点坐标为(3,0),(5,0),又因为以函数与x轴,y轴交点为顶点的三角形面积为3,可得与y轴的交点的坐标为(0,3).利用交点式y=a(x-x
1)(x-x
2),求出解析式.
点评:本题主要考查用待定系数法求二次函数的解析式,此题是开放题,解题的关键理解题意.还要注意利用待定系数法求函数解析式,当题目中出现二次函数与x轴的交点坐标时,采用交点式比较简单.

 ②
②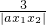 ,
,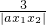 ,
,

 (x-7)(x-1)或y=±
(x-7)(x-1)或y=± (x-5)(x-3)
(x-5)(x-3) x2-
x2- x+1,
x+1, x2+
x2+ x-1.
x-1. x2-
x2- x+3,
x+3, x2+
x2+ x-3.
x-3. x2-
x2- x+3(答案不唯一).
x+3(答案不唯一).
